Editor’s Note: Published in 1956, this article proved so popular that it served as the inspiration for Martin Gardner’s legendary Scientific American column Mathematical Games. Read more in our special digital issue, Fun and Games.
Mathematics owes a lot to games, and vice versa. There is an engaging little exercise with strips of paper which has fascinated some first-class brains in recent years. It was discovered in an idle moment by a British mathematics student at Princeton University. The whole thing grew out of the trivial circumstance that British and American notebook paper are not the same size. Arthur H. Stone, a 23-year-old English graduate student who came to Princeton on a fellowship in the fall of 1939, found that he had to trim an inch off American notebook sheets to fit them into his English binder. For amusement he began to fold the trimmed-off strips of paper in various ways, and one of the figures he made turned out to be particularly intriguing. He had folded the strip diagonally at three places and joined the ends so that it made a hexagon [see illustration below]. When he pinched two adjacent triangles together and pushed the opposite vertex of the hexagon toward the center, the hexagon would open out again, like a budding flower, and show a completely new face. If, for instance, the top and bottom faces of the original hexagon were painted different colors, the new face would come up blank and one of the colored faces would disappear!
[Play science-inspired games, puzzles and quizzes in our new Games section]
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
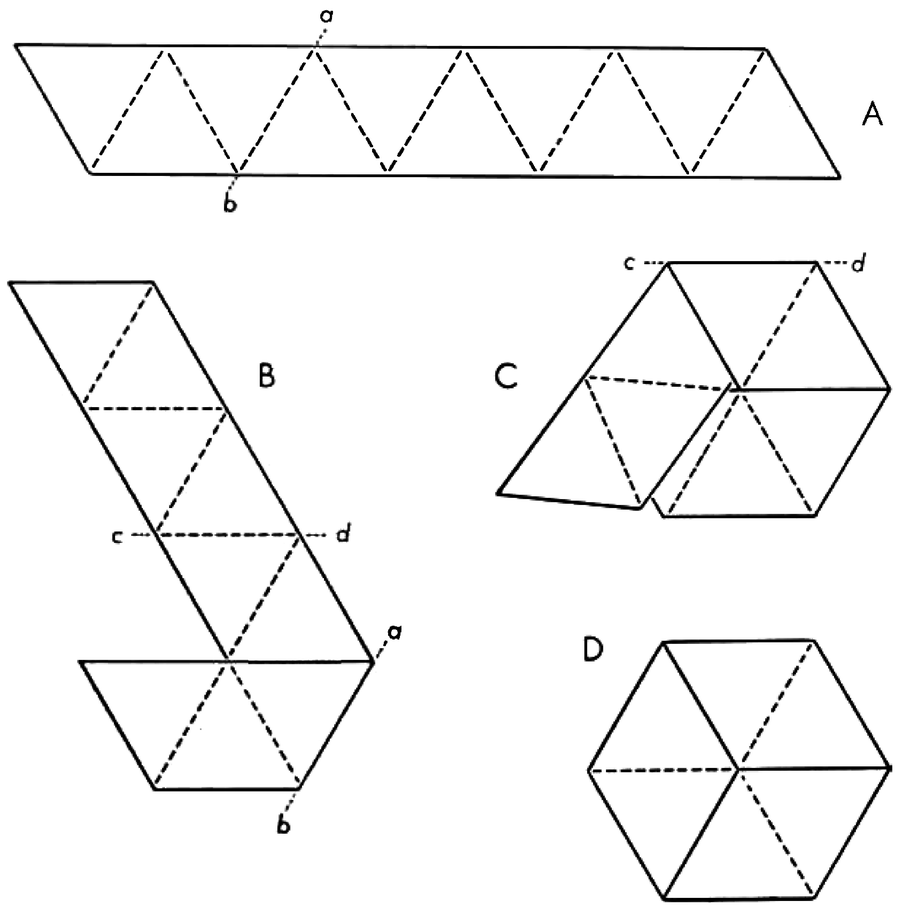
Trihexaflexagon is constructed by cutting a strip of paper so that it may be marked off in 10 equilateral triangles (A). The strip is folded backward along the line ab and turned over (B). It is then folded backward again along the line cd and the next to the last triangle placed on top of the first (C). The last triangle is now folded backward and glued to the other side of the first (D). The figure may be flexed as shown below. It is not meant to be cut out. Fairly stiff paper at least an inch and a half wide is recommended.
Bunji Tagawa
This figure had three faces—say, red, green and blank. Stone experimented further with longer strips, and, with considerable patience and creative insight, was able to construct a model which had the same hexagonal shape but could be opened to six different faces instead of only three. At this point Stone found the game so interesting that he showed his paper models to friends in the graduate school. Soon “flexagons” were appearing in profusion at the lunch and dinner tables. A “Flexagon Committee” was organized to probe further into the mysteries of flexigation. The other members besides Stone were Bryant Tuckerman, a graduate student of mathematics; Richard P. Feynman, a graduate student in physics; and John W. Tukey, a young mathematics instructor.
The models were named hexaflexagons—“hexa” for the six triangles that form the hexagonal face, and “flexagon” for the structure’s ability to flex. Stone’s first model is a trihexaflexagon (“tri” for the three different faces that can be brought into view); his elegant second structure is a hexahexaflexagon (for its six faces).
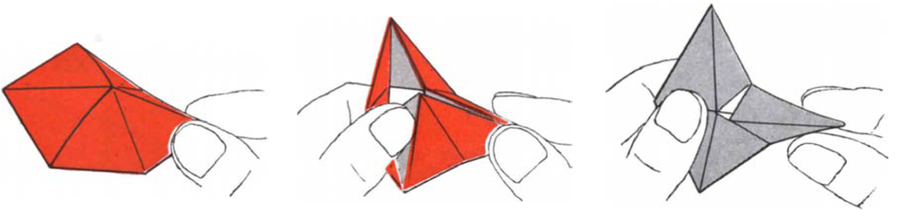
Trihexaflexagon is flexed by pinching together two of its triangles. The inner edge of the two opposite triangles may be opened with the other hand (middle). If the figure cannot be opened, the adjacent pair of triangles is pinched. If the figure opens, it can be turned inside out, revealing a side that was not visible before.
Bunji Tagawa
To make a hexahexaflexagon you start with a strip of paper (the tape used in adding machines serves admirably) which is divided into 19 triangles [see illustration below]. You number the triangles on one side of the strip 1, 2 and 3, leaving the 19th triangle blank, as shown in the drawing. On the opposite side of the triangles are numbered 4, 5 and 6, according to the scheme shown. Now you fold the strip so that the same underside numbers face each other—4 on 4, 5 on 5, 6 on 6 and so on. The resulting folded strip, illustrated by the second drawing below, is then folded back on the lines ab and cd [third drawing in illustration], forming the hexagon [fourth drawing in illustration]; finally the blank triangle is turned under and pasted to the corresponding blank triangle on the other side of the strip. All this is easier to carry out with a marked strip of paper than it is to describe.
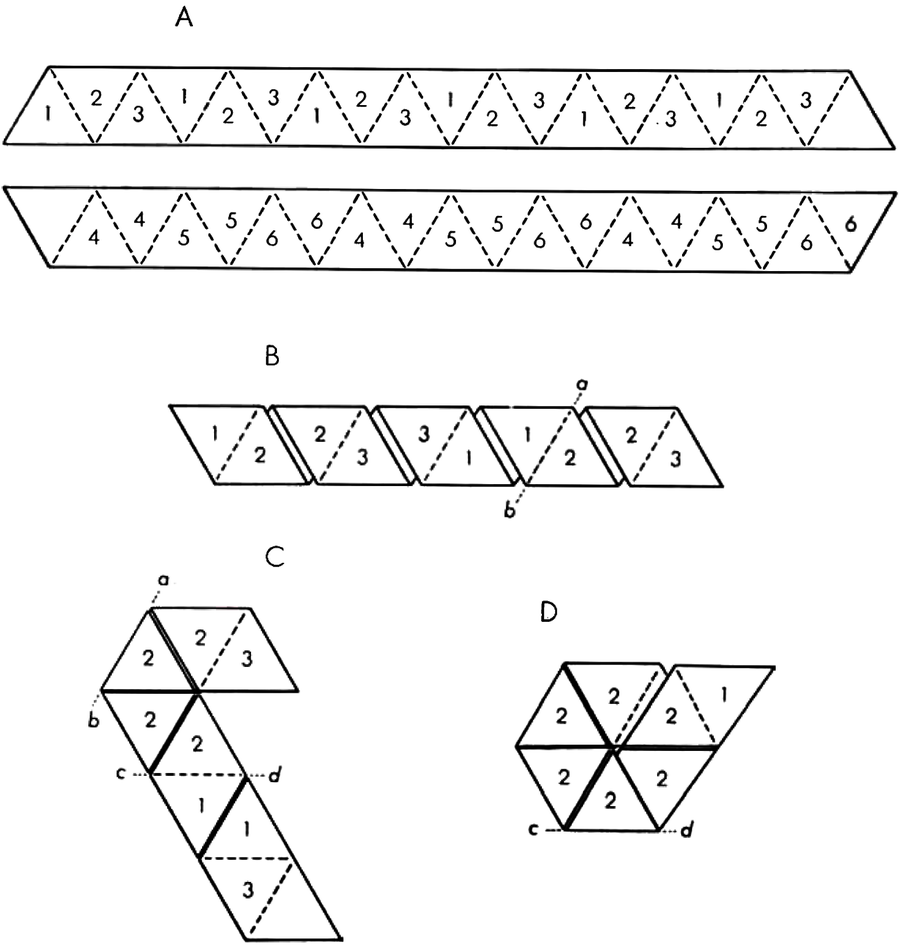
Hexahexaflexagon is constructed by cutting a strip of paper so that it may be marked off in 19 triangles (A). The triangles on one side are numbered 1, 2 and 3; the triangles on the other, 4, 5 and 6. A similar pattern of colors or geometrical figures may also be used. The hexagon is then folded as shown. The figure can be flexed to show six different faces.
Bunji Tagawa
If you have made the folds properly, the triangles on one visible face of the hexagon are all numbered 1, and on the other face all are numbered 2. Your hexahexaflexagon is now ready for flexing. You pinch two adjacent triangles together, bending the paper along the line between them, and push in the opposite vertex; the figure may then open up to face 3 or 5. By random flexing you should be able to find the other faces without much difficulty. Faces 4, 5 and 6 are a bit harder to uncover than 1, 2 and 3. At times you may find yourself trapped in an annoying cycle that keeps returning the same three faces over and over again.
Tuckerman quickly discovered that the simplest way to bring out all the faces of any flexagon was to keep flexing it at the same vertex until it refused to open, then to shift to an adjacent vertex. This procedure, known as the “Tuckerman traverse,” will bring up the six faces of a hexahexa in a cycle of 12 flexes, but 1, 2 and 3 turn up three times as often as 4, 5 and 6.

“Tuckerman’s Traverse” exposes all six faces of a hexahexaflexagon in 12 flexes. Here the numbers of the flexagon in the preceding image have been replaced by geometrical figures in the same pattern. Faces 1, 2 and 3 turn up three times as often as faces 4, 5 and 6.
Bunji Tagawa
By lengthening the chain of triangles, the Committee discovered, one can make flexagons with 9, 12, 15 or more faces: Tuckerman managed to make a workable model with 48! He also found that with a strip of paper cut in a zigzag pattern (i.e., a strip with sawtooth rather than straight edges) it was possible to produce a tetrahexaflexagon (four faces) or a pentahexaflexagon. There are three different hexahexaflexagons—one folded from a straight strip, one from a chain bent into a hexagon and one from a form that somewhat resembles a three-leaf clover. The decahexaflexagon (10 faces) has 82 different variations, all folded from weirdly bent strips. Flexagons can be formed with any desired number of faces, but beyond 10 the number of different species for each increases at an alarming rate. All even-numbered flexagons, by the way, are made of strips with two distinct sides, but those with an odd number of faces have only a single side, like a Moebius surface.
A complete mathematical theory of flexigation was worked out in 1940 by Tukey and Feynman. It shows, among other things, exactly how to construct a flexagon of any desired size or species. The theory has never been published, though portions of it have since been rediscovered by other mathematicians. Among the flexigators is Tuckerman’s father, the distinguished physicist Louis B. Tuckerman, who was formerly with the National Bureau of Standards. Tuckerman senior devised a simple but efficient diagrammatic notation for the theory.
Pearl Harbor called a halt to the Committee’s flexigation program, and war work soon scattered the four charter members to the winds. Stone is now a lecturer in mathematics at the University of Manchester in England. Feynman, now at the California Institute of Technology, is a famous theoretical physicist. Tukey, a professor of mathematics at Princeton, has made brilliant contributions to topology and to statistical theory which have brought him worldwide recognition. Tuckerman is a well-known mathematician at the Institute for Advanced Study in Princeton, where he works on the Institute’s electronic computer project.
One of these days the Committee hopes to get together on a paper or two which will be the definitive exposition of flexagon theory. Until then the rest of us are free to flex our flexagons and see how much of the theory we can discover for ourselves.
