October 12, 2024

Math Puzzle: Play Architect with These Houses of Cards

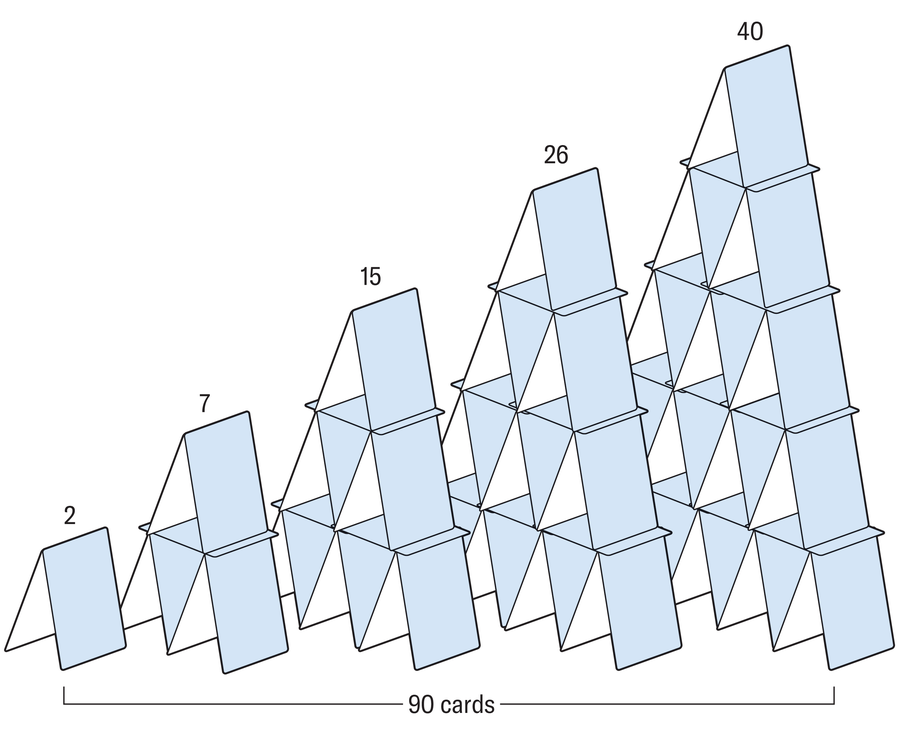
Jovan built these five houses of cards using a total of exactly 90 playing cards. Now he wants to build one large house consisting of exactly 100 cards. Can such a house of cards exist?

Graphic shows five triangle-shaped houses of cards composed of the following numbers of cards: 2, 7, 15, 26 and 40. The total number of cards shown is 90. — Amanda Montañez; Source: Hans-Karl Eder/*Spektrum der Wissenschaft* (reference)

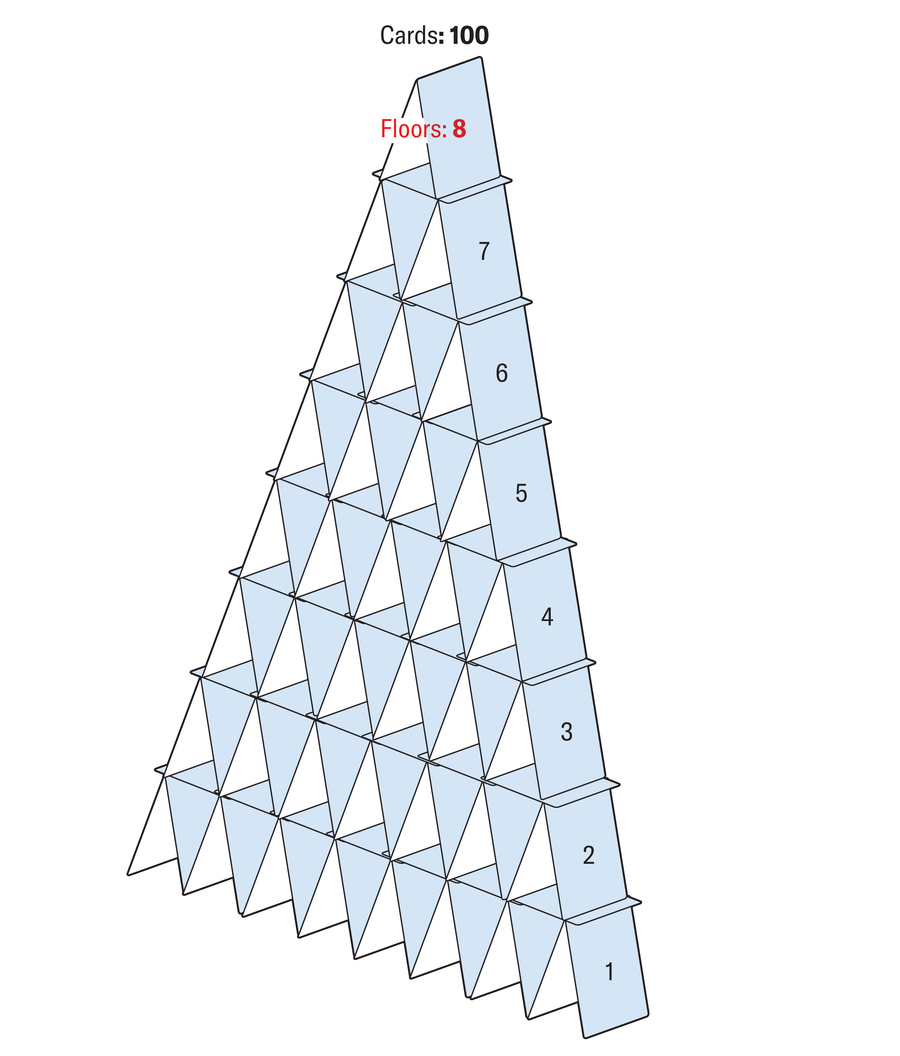
You can build a house of cards with exactly 100 cards; it will have eight floors.

Graphic shows a triangle-shaped house of cards that has eight floors and is composed of 100 cards. — Amanda Montañez; Source: Hans-Karl Eder/Spektrum der Wissenschaft (*reference*)

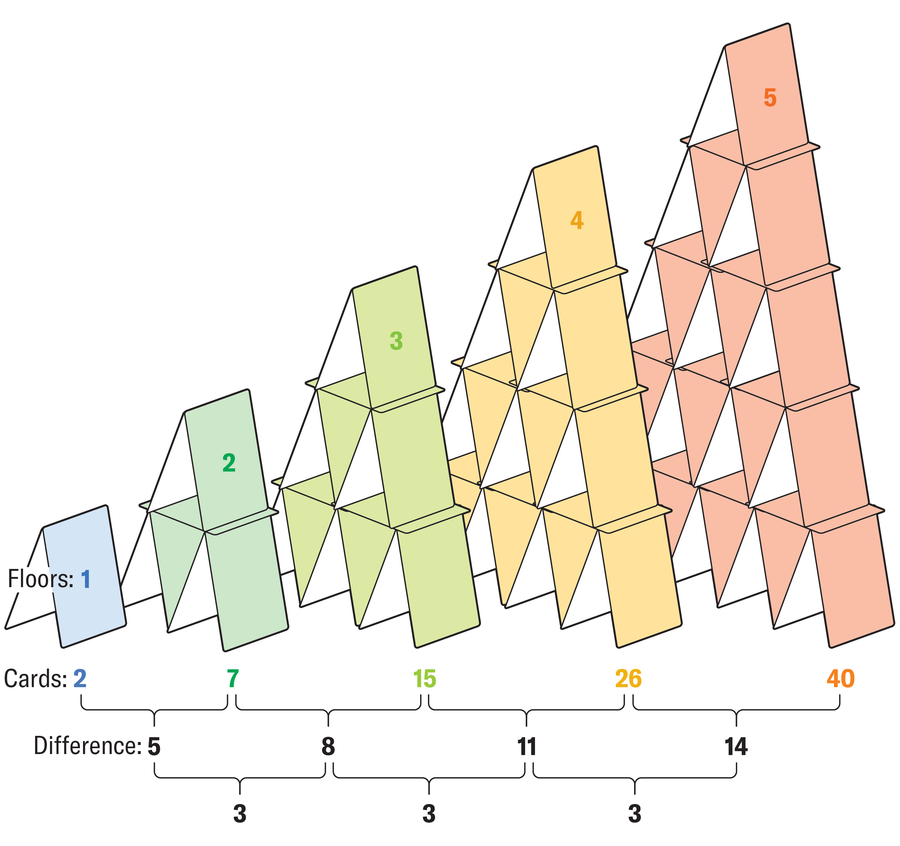
The number of cards increases level by level in a constant sequence. If you want to prove the puzzle’s answer, you have to show that 100 is a term in this sequence.

Graphic shows five triangle-shaped houses of cards composed of 2, 7, 15, 26 and 40 cards. The number of floors in each house is highlighted: 1, 2, 3, 4 and 5. The increase in the number of cards at each step is shown (7 minus 2, 15 minus 7, and so on), followed by the difference between each of those increases (8 minus 5, 11 minus 8, and so on), which equals 3. — Amanda Montañez; Source: Hans-Karl Eder/*Spektrum der Wissenschaft* (*reference*)

Here's one way to do it. Because the difference between terms always changes the same amount—the “second difference” is constant—you can conclude that the sequence, with number of cards K and number of floors x, can be represented by a quadratic equation of the form K = ax²+ bx + c.

First, determine the values for a, b and c. This can be achieved using a system of three equations:

A system of three equations is created from the first three terms in the house of cards sequence: 2 equals a times 1 squared plus b times 1 plus c; 7equals a times 2 squared plus b times 2 plus c; 15 equals a times 3 squared plus b times 3 plus c. Subtracting the first equation from the second one gives an equation designated capital A: 5 equals 3a + b. And subtracting the second equation from the third one gives an equation designated capital B: 8 equals 5a plus b. Subtracting equation capital A from equation capital B allows you to calculate that a equals 1.5. And inserting that into equation capital B lets you find that b equals 0.5. Combining those values for a and b with your original first equation, 2 equals a plus b plus c, reveals that c equals 0. — Amanda Montañez; Source: Hans-Karl Eder/*Spektrum der Wissenschaft* (reference)

With the values found for a, b and c and the calculated value for K = 100, you can now solve the quadratic equation.

Graphic 5 alt text: Now you can insert the number of cards K equals 100 into the quadratic equation K equals a times x squared plus b times x plus c. Using the values you found earlier, you get the equation 100 equals 1.5 times x squared plus 0.5 times x plus 0. Divide both sides by 1.5 and move all terms to one side to find x squared plus one third times x minus 200 thirds equals 0, which is equivalent to x minus 8 times x plus 25 thirds equals 0. Therefore, x equals 8 or negative 25 thirds. — Amanda Montañez; Source: Hans-Karl Eder/*Spektrum der Wissenschaft* (reference)

One of the values for x is a natural number that lets you build a house of cards out of exactly 100 cards.

We’d love to hear from you! E-mail us at games@sciam.com to share your experience.

This puzzle originally appeared in Spektrum der Wissenschaft and was reproduced with permission.