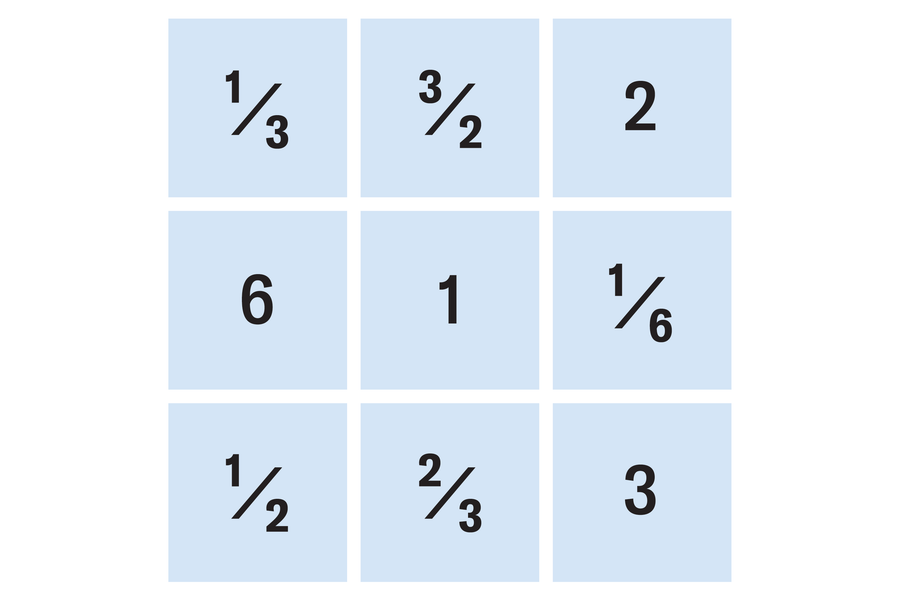
Distribute the numbers 1⁄6, 1⁄3, 1⁄2, 2⁄3, 1, 3⁄2, 2, 3 and 6 among the nine fields of the grid below so the product of the three numbers in each row, each column and each of the two diagonals is the same.

Spektrum der Wissenschaft, restyled by Amanda Montañez
The product of all nine numbers is 1⁄6 × 1⁄3 × 1⁄2 × 2⁄3 × 1 × 3⁄2 × 2 × 3 × 6 = 1, so the product of each of the eight expressions should also be 1. There are a total of eight possibilities in which three of these numbers result in the product 1. These are 1⁄6 × 1 × 6, 1⁄6 × 2 × 3, 1⁄3 × 1⁄2 × 6, 1⁄3 × 1 × 3, 1⁄3 × 3⁄2 × 2, 1⁄2 × 2⁄3 × 3, 1⁄2 × 1 × 2 and 2⁄3 × 1 × 3⁄2. The middle field of the square is included in four expressions; because 1 is the only number that appears in four possibilities, it must be in the middle field. The corners of the square belong to three expressions each, and because 1⁄3, 1⁄2, 2 and 3 only appear three times each, these numbers must be on the corner squares. The rest is straightforward—there is just one solution, apart from mirroring and rotating the pattern.
Spektrum der Wissenschaft, restyled by Amanda Montañez
We’d love to hear from you! E-mail us at games@sciam.com to share your experience.
This puzzle originally appeared in Spektrum der Wissenschaft and was reproduced with permission.