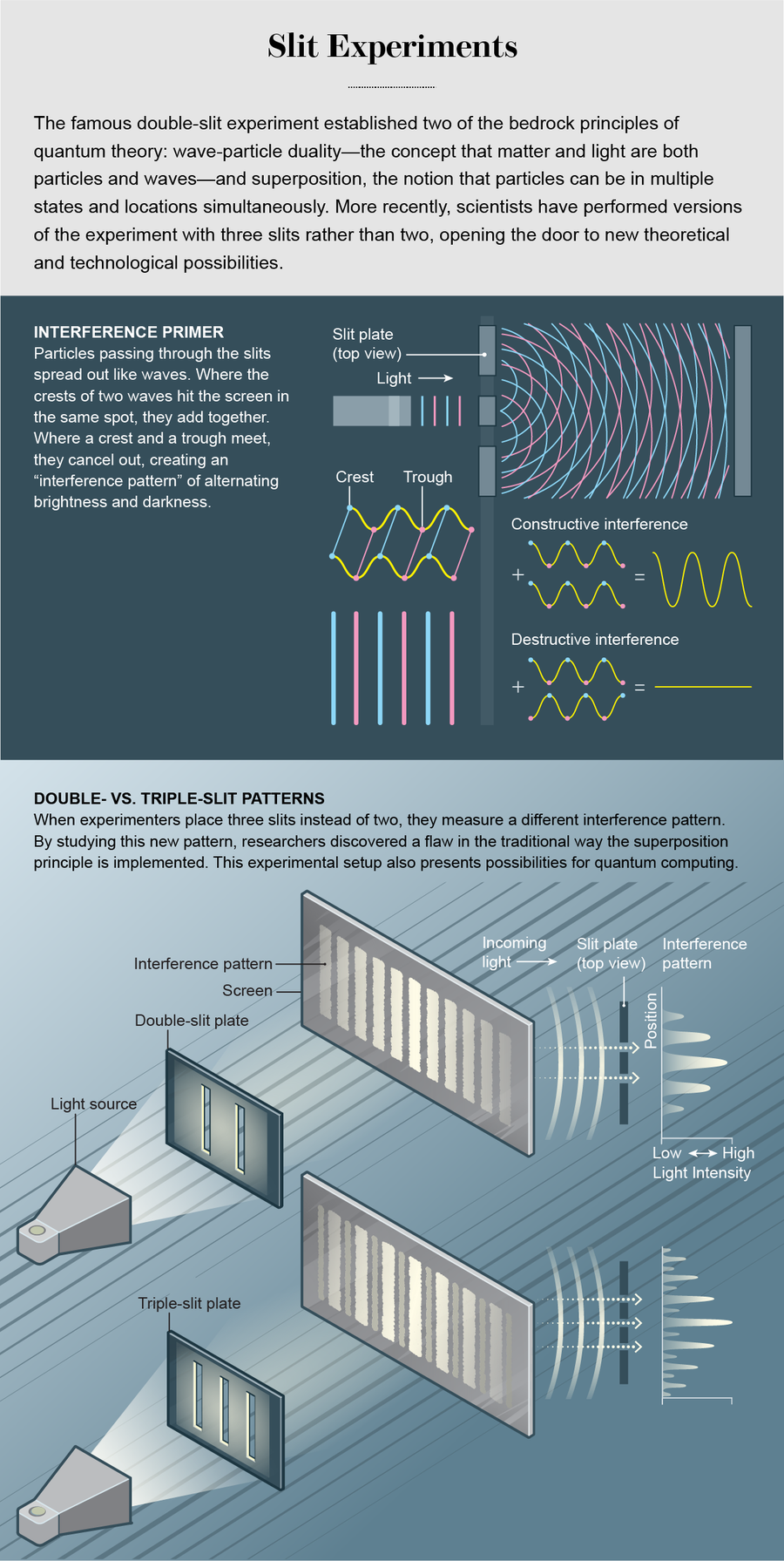
“All of the mystery of quantum mechanics” is contained within the double-slit experiment, Nobel laureate Richard Feynman famously said. In the experiment, first proposed in 1801 by British polymath Thomas Young, a beam of photons—particles of light—flies toward a wall with two slits cut in it. When the light reaches a screen behind the wall, it produces a telltale “interference pattern”: stripes of light interspersed with darkness. This pattern results only if the photons act like waves rather than like point particles, and the peaks and troughs of the waves coming through the two slits interfere with one another, sometimes adding light and sometimes canceling it out. When Young performed the experiment, using a modified setup, it seemed to establish that light was a wave and not a particle.
Or was it? Weirdly, in experiments centuries later in which researchers took care to shine only one photon at a time toward the wall, the interference pattern remained, as if a single particle were interfering with itself. Even stranger, if you place a detector by the slits to record which slit each particle passes through, the interference pattern disappears. Instead you get two lines of light on the screen, just what you would expect if point particles and not waves were passing through—as if the act of measurement changed the nature of the particles.
To this day, the double-slit experiment, with its inherent simplicity of concept, remains one of the most intriguing tests ever performed. It has been repeated many times, with particles of both light and matter. It clearly demonstrates the fundamental strangeness of quantum mechanics: that light, and matter as well, is in fact both a particle and a wave—a concept known as wave-particle duality. It also establishes the superposition principle: particles can exist in multiple states and even simultaneously in multiple places. In the double-slit experiment, particles must not be traveling through one slit or the other—for interference to occur, each particle must be traveling through both.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
As celebrated as this experiment is, we have not yet plumbed its depths. Recently my team at the Quantum Information and Computing laboratory at the Raman Research Institute in Bangalore, India, has set up “triple-slit” experiments in the microwave-wavelength range—instead of two slits, we use three. It is a seemingly simple adjustment, but it has profound consequences. On the theory side, our triple-slit trials have clarified how the superposition principle applies in these circumstances and have revealed new subtleties in our fundamental understanding of this phenomenon.
Our triple-slit experiment architecture also offers intriguing opportunities in the emerging field of quantum computing. Quantum computers promise to enable calculations that were previously intractable—if we can harness the power of quantum physics to build them. One of the central challenges in quantum computing is finding a way to increase the number of bits a quantum computer contains, called qubits, without destroying the superposition that allows qubits to be in two states at once—the key to achieving huge gains in computing speed. Whereas most of the community is working on increasing the number of qubits in a system, my lab is trying an alternative, less explored approach by using higher-dimensional “qudits” instead of two-dimensional qubits. Using the triple-slit system, we can create three-dimensional qudits called qutrits.
Credit: Nick Bockelman
The Superposition Principle
Quantum theory describes fundamental particles not just as physical waves but also as being determined by the so-called wave equation, whose solutions may be designated by the Greek letter psi, Ψ. These solutions express the probability amplitude of the particle being in any particular state.
Our research, however, has revealed a flaw in the way physicists have traditionally dealt with wave-equation calculations when they are applied to the double-slit experiment. Imagine the classic experiment and let the two slits be named A and B, respectively. The solutions to the wave equation describing a particle in this system can be labeled ΨA when slit A is open and ΨB when slit B is open. What happens when both slits are open? It is common practice in textbooks to call the solution ΨA + ΨB to represent the fact that the particle is in a superposition state in which it is passing through both slits. This is indeed an application of the superposition principle, though an incomplete one. The reason is simple: The situation with two slits open at once is not the same as the combination of having the slits open separately. We know that when they are open at the same time, a particle in some ways passes through both and interacts with itself, and we cannot represent these interactions by simply adding the two solutions.
Scientists have suggested before that some correction term might be needed to make our equations accurate. This quantity is called the Sorkin parameter because it was predicted in 1994 by physicist Rafael Sorkin, then at Syracuse University. Most researchers, however, have assumed that this term would be so small as to be negligible. And indeed, we know it cannot be too large, or it would have been observed much earlier. But our triple-slit experiment proved that this term does exist and that it is not always small enough to be ignored. The use of three or more slits provides us with a natural test bed for this correction term because we can measure a quantity (the Sorkin parameter) that will be zero if the correction term does not exist and nonzero if it does exist. (In the two-slit case, the correction term gets added to something that is already nonzero, so it does not show up in a noticeable way.)
I have been working on triple-slit experiments for more than a decade. In 2010 my colleagues and I published our first results in a paper in Science. In 2014 my team and I began to run new trials of our triple-slit experiment using microwaves at the Gauribidanur astronomical observatory in Karnataka, India. We carried out the project in an open field in a tent next to corn crops. Although the setting might sound odd for a precision physics experiment, the corn provided a good source of absorption for stray microwaves that might have interfered with our measurements. It also helped that we were not working with walls or lots of equipment in the space that could reflect waves. Furthermore, our isolated location had poor cell service—another benefit in avoiding contamination—and we were able to run our experiment on a very large scale.
Our setup used two horn antennas—one to release microwave photons and one to detect them. Between them was a plate with three slots, each 10 centimeters wide, spaced 13 centimeters apart. Staying true to the style of the first slit-based experiments, we housed the detector on a rail that we could move to measure the different interference patterns as a function of detector position. We found that the interference pattern we measured did not match the approximate solution to the wave equation given by ΨA + ΨB, but it did match the solution that included the nonzero Sorkin parameter. We also used a blocking material to obstruct the space between the slits, essentially stopping the photons from traveling between the slits and interacting with the neighboring slits. When we did this, we saw that the value of the Sorkin parameter changed with the size of the block—showing that the parameter indeed measures interactions between the slits and that it varies depending on the level of interactions. This finding established that the correction term we measured was not some systematic error from our experiment that we had failed to understand but was indeed the thing we were looking for.
Ours was the first definitive validation of the Sorkin parameter as a correction term to the superposition principle in the classical microwave domain. The results, published in June 2018 in the New Journal of Physics, have already led to some textbook edits, and they affect our basic understanding of fundamental physics. They might also have implications for work being done in astronomy and astrophysics to study signals from the early universe. This research often involves arrays of radio antennas spread over the ground. Commonly, the data received by the different antennas are added together. But now that we know the wave-equation solution is not just the sum of the individual solutions, some calculations may need to be updated with the correct Sorkin parameter. Our findings might eventually help scientists develop better error models for these observations.
Credit: Nick Bockelman
Quantum Qutrits
Our experiment is interesting not only theoretically but also perhaps practically as well. We hope to use our triple-slit process to help design new tools for quantum computing.
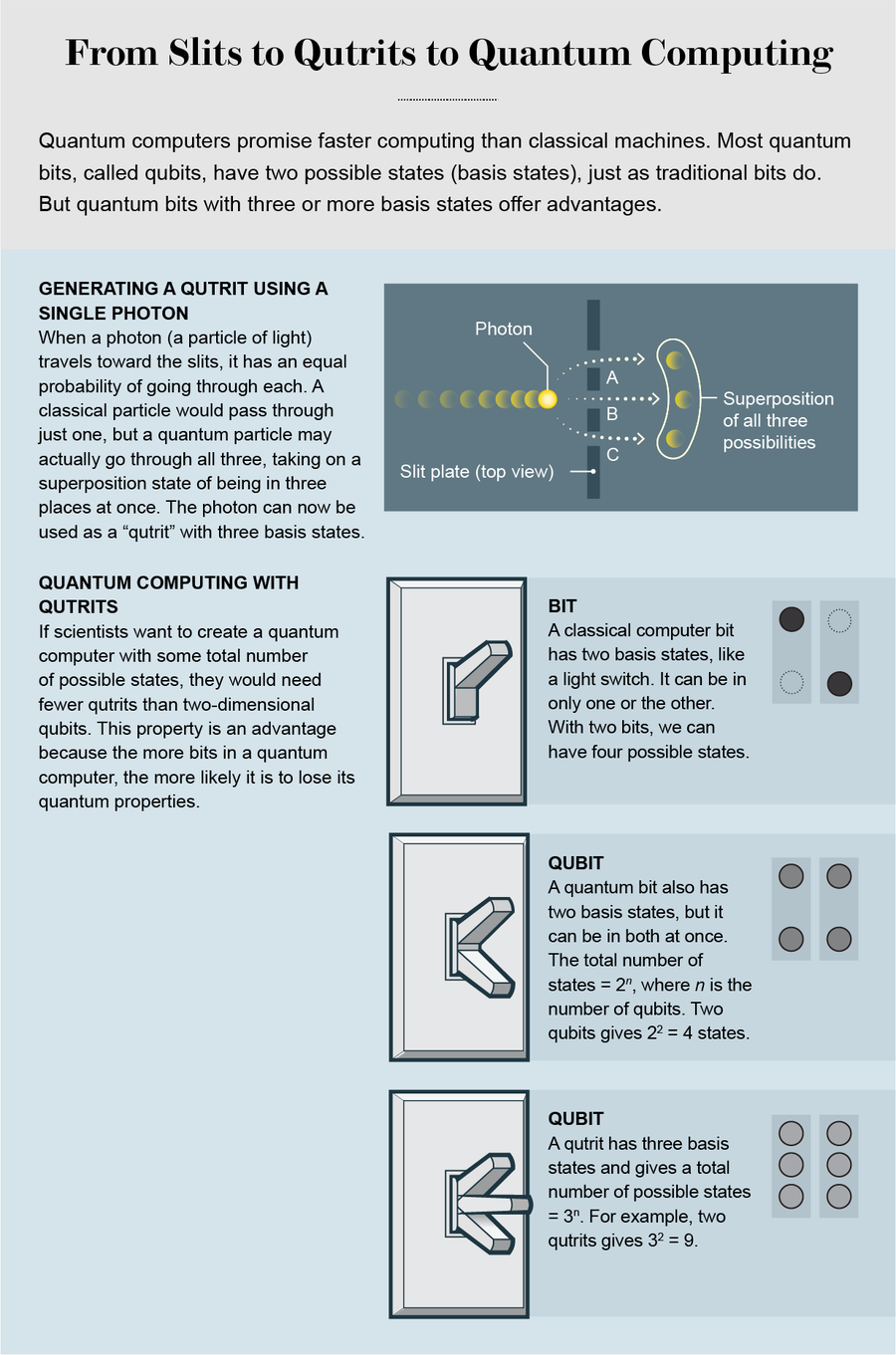
Quantum computers take advantage of quantum laws such as superposition to enable computations much quicker than those of classical machines. Consider a traditional computer bit as if it were a light switch: it can be either “on” or “off” (corresponding to a value of 1 or 0, respectively, in binary code). In the quantum world, though, a switch need not be either on or off—it can be both. In a qubit, we define a state with a finite probability of being in the on state and in the off state at the same time. This combination of both states with some probability of each is the essence of superposition.
The two states that contribute to the superposition state are called the basis states. A regular qubit has two basis states, and for n qubits one has access to 2n possible states. Thus, with two qubits, there are 22 = 4 possible states. Whereas for n classical bits the state occurs in only one of the 2n possibilities, for n quantum bits all 2n possibilities can coexist. The power of quantum computing comes from cleverly designed quantum algorithms that can make use of the superposition state during execution and perform a certain class of operations at exponentially higher speeds than a classical computer.
Yet to reach this goal, we need a reasonably high number of qubits—certainly more than just two. One number many in the community have begun working toward is n = 50, which offers many interesting possibilities for quantum algorithms.
With 50 qubits, we have 250 possible states available for quantum operations. Recently Google claimed it had achieved this milestone by successfully implementing a random sampling calculation on a 54-qubit quantum processor. Getting to large numbers of qubits, however, is easier said than done. The more qubits we put together, the greater the chance they will lose their special quantum ability for superposition and collapse back into normal, classical bits. This happens when a qubit interacts with the outside environment and loses “coherence.” As we try to get more qubits into a coherent superposition, it becomes more and more difficult to maintain this state for long. It is much like putting people into a room for a party. If you have 10 people in a 100-square-foot room, there is enough area for them to coexist without getting into one another’s space. If we increase the number of people to 30, some crowding starts, which leads to a general loss of peaceful coexistence. The same thing happens with qubits.
One alternative to the usual strategy is to increase the dimension of each quantum bit rather than trying to fit more qubits into the same space. To see why this helps, let us go back to an elementary mathematics problem:
What is 23? The answer is, of course, 8 (2 × 2 × 2 = 8).
Now, what is 32? The answer here is 9 (3 × 3 = 9).
These results are of the same order of magnitude—quite close. Thus, instead of three qubits, if we were to use two qutrits—that is, three-dimensional quantum bits—we would have access to a similar number of possible states. So instead of trying to increase the exponent, why not try to change the base? If we increase the number of basis states, we will need a smaller number of bits to achieve the same goal. This realization is what defines research in higher-dimensional quantum systems.
And our strategy has another benefit: we are no longer bound by binary code. Consider the outcome of a game of football. Usually we think of two outcomes, “win” and “loss,” which can be specified using two states, so in a quantum world a qubit is sufficient. If we add two more possible outcomes, say, “abandoned” and “draw,” one qubit is not enough to declare the results. We need two qubits. But if we had a four-state system, one would be enough. Such a system would be a “ququad.”
Higher-dimensional quantum systems, or qudit systems, can thus pack more information in a smaller number of systems. This benefit has been theoretically proved to offer an advantage with respect to a certain goal for quantum computers—namely, creating hack-proof communication using so-called quantum key distribution. In this method, two parties create a shared secret “key” that only they can use to decode messages. If you can increase the dimension of your quantum bits by increasing the number of basis states, the result is a key that is more resistant to certain kinds of attacks. In addition to the possibility of higher security in key distribution, qudits also promise a greater amount of randomness in true random number generation—another hoped-for application of quantum computers.
Despite these benefits, qudit-based systems have some drawbacks. It is hard to actually come up with stable physical systems in which all the basis states are equally easy to reach. For instance, sometimes a system may be biased toward its lowest-energy, or ground, state, and resulting calculations could carry this bias. A second hurdle is simply that this line of research is newer than qubits, so fewer algorithms and tools have been developed for qudits. Although there is a lot to be done, the number of open problems makes this research exciting and rich in potential.
Toward a Quantum Computer
So how do we get from our basic triple-slit experiment to a working qutrit system? The first step is to generate single photons.
We start with a very strong laser beam, which we shine toward a special crystal material. Under certain conditions, one in about 108 to 1010 photons splits into two photons of lower energy in a process called down conversion. The daughter photons always appear as a pair. We measure one of the photons using a single-photon detector, and this measurement heralds the presence of the other photon because we know they were produced simultaneously. We can then use the second photon for experiments.
In our team’s work, we have played with the characteristics of the “mother” photon to ensure that the daughter photons share its characteristics. The mother photon is directed at three slits, and its spatial profile then mimics the triple-slit profile. The daughter photons in turn carry this profile through. The photon enters a superposition that gives us a “spatial-bin” qutrit whose three basis states are the three slit positions.
Still, this qutrit we have created is a far cry from what is needed for a functional quantum computer. We would need to use our slit system to generate numerous qutrits and then feed them into an architecture with so-called gate operations capable of using the qutrits to perform calculations. This area is the focus of my team’s current efforts. We must design the specific optical elements needed to accomplish this manipulation and then miniaturize everything so that it can define a working computer system.
Triple slits therefore represent the yin and the yang of physics research—both fundamental and functional. Our research on the superposition principle and its first measured correction term explores the very basic concepts of physics. Meanwhile triple-slit-based qudits represent a technological feat in the advancement toward higher-dimensional quantum computing and quantum communications. This most famous of physics experiments, it turns out, is still offering new insights and possibilities.”

