In November 2022 a colleague of mine casually asked what I was working on. My dazed answer reflected the swirl of ideas that was consuming all my mental energy at the time: “Actually, I think the solution to a major open problem just fell into my lap.” A week before, I had received an e-mail asking me to look at a shape. That was the first time I saw “the hat,” an unassuming polygon that turned out to be the culmination of a decades-long mathematical quest.
The e-mail came from David Smith, someone I knew from a small mailing list of people interested in tilings—different ways to arrange shapes to cover a flat surface. Smith isn't a mathematician; he is a self-professed “shape hobbyist” who experiments with geometry in his spare time from his home in Yorkshire, England. After Smith sent me the hat shape he'd been playing with, we began corresponding regularly, spending the rest of 2022 studying the hat and its properties. In 2023 we reached out to two additional researchers, mathematician Chaim Goodman-Strauss and software developer Joseph Samuel Myers, both also members of the mailing list and well known in the larger world of tiling theory. The four of us continued to study the hat and, in what felt like record time, succeeded in proving that the shape was a long-sought object that many assumed couldn't exist: an aperiodic monotile, also known as an einstein tile.

Credit: Jen Christiansen
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
As it turns out, Smith's hat was just the beginning of a sequence of revelations. As we explored the new landscape of ideas revealed by this shape, we were surprised multiple times by additional discoveries that further deepened our understanding of tiling theory. Soon the hat led to “turtles,” “spectres,” and other wonders that yielded more insights than we could have expected at the outset.
Tiles have fascinated humans since ancient times, but mathematicians began studying them in earnest in the 20th century. A so-called tiling of the plane is an infinite collection of shapes that cover a flat surface with no gaps and no overlaps. I will focus on cases where the infinitely many tiles in a tiling come in a finite number of distinct shapes. Imagine a handful of templates that can be used to cut copies of the shapes out of an unlimited supply of paper. Our goal is to arrange cutouts on an infinite tabletop so that every bit of table is covered by exactly one layer of paper. We can move each cutout into position through some combination of reflection (flipping the paper over), rotation (turning it in place) and translation (sliding the shape around without turning it). If we achieve our goal of constructing a tiling, we say that the set of shapes “admits” the tiling and, more generally, that the shapes tile the plane.
Not all sets of shapes admit tilings. A square yields a tiling resembling graph paper, among other patterns, and is therefore a monotile: it tiles the plane on its own (as a set of one). A regular pentagon, in contrast, cannot tile the plane by itself. Neither can a regular octagon, although a two-element set consisting of an octagon and a square does tile.
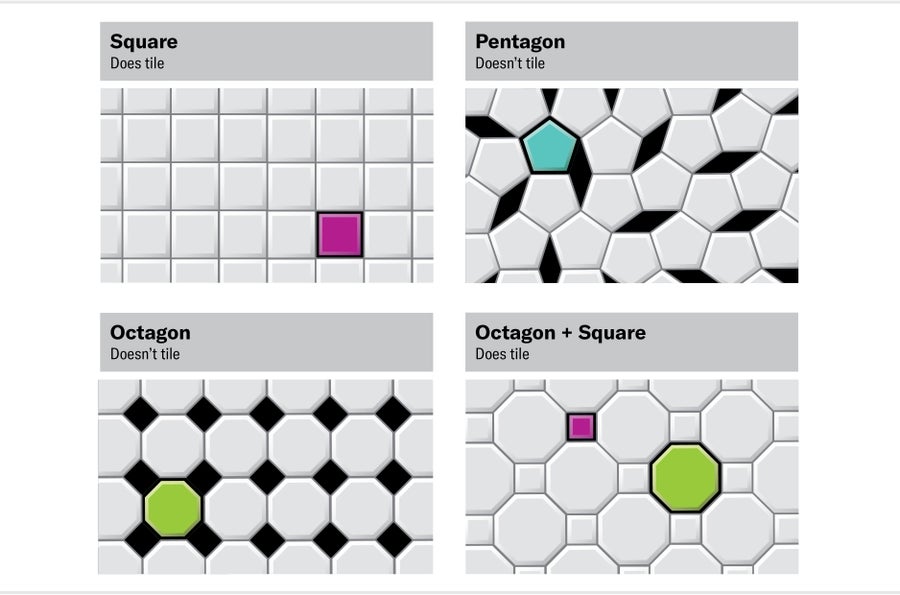
Credit: Jen Christiansen
How can we determine whether a given set of shapes tiles the plane? There's no algorithm we can use to answer this question, and in fact none could exist—the problem is what's known in theoretical computer science as “undecidable.” Nevertheless, we can study individual sets and attempt to build tilings through trial and error or other methods. Along the way we often encounter fascinating examples of how local interactions (the different ways two tiles can sit side-by-side) influence global behavior (the large-scale structure of the tiling out to infinity in every direction).
There are multiple ways to figure out whether a single shape can tile the plane. Some people, such as Smith, will even cut out physical paper copies of a shape using a computer-controlled cutting tool and play with them on actual (regrettably finite) tabletops, recruiting the immediacy of touch to augment visual intuition. In the hands of a skilled explorer like Smith, a shape will disclose its tiling secrets in short order. And in the pre-hat era, a shape would invariably behave in one of two ways.
The first possibility is that the shape will not tile the plane. As a quick test, we might try to surround it completely by copies of itself; if we can't, then the shape certainly does not admit any tilings. For instance, the regular pentagon is unsurroundable, which immediately outs it as a nontiler. But although surroundability provides evidence of tilability, it is not firm proof: there are deceptive nontilers that can be completely surrounded by one or more concentric layers of copies before getting irretrievably stuck. In 1968 mathematician Heinrich Heesch exhibited a shape that could be surrounded once but not twice and asked whether there was an upper limit to the number of concentric rings one might build around a nontiler, a quantity now known as a shape's “Heesch number.” The current record holder is a particularly ornery polygon with a Heesch number of six, discovered in 2020 by Bojan Bašić of the University of Novi Sad in Serbia.
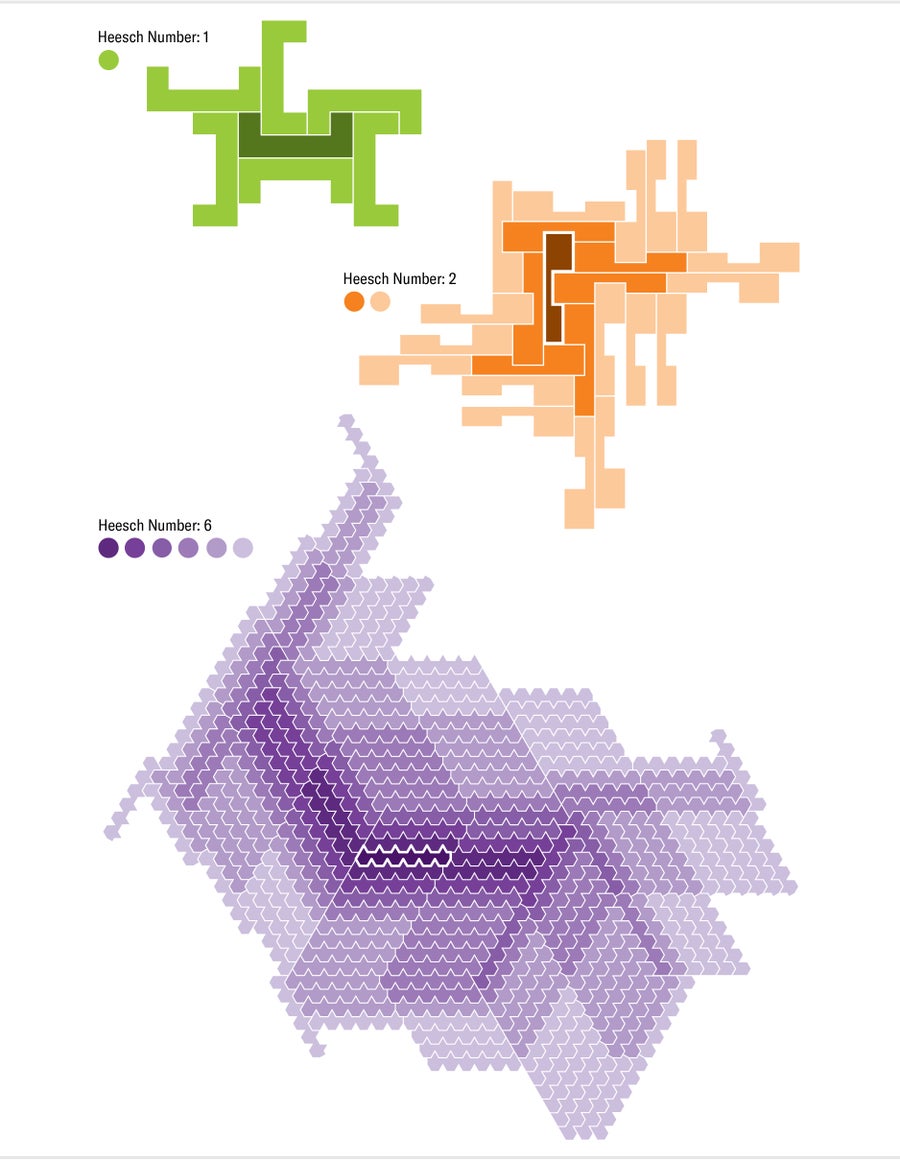
Credit: Jen Christiansen
The second possibility is that the shape tiles the plane periodically. In a periodic tiling, the arrangement of tiles repeats in a regular pattern determined by an infinite grid of parallelograms. We can describe a periodic tiling using three pieces of information: a finite cluster of tiles called a translational unit and two line segments that define the sides of a parallelogram in the grid. We can slide a copy of the translational unit out to every vertex in the grid, without rotating or reflecting it, and these copies will interlock to complete a tiling. This method offers a quick test of a shape's ability to tile: we assemble candidate translational units and then see whether any of them covers the plane by repeating in a regular grid. As with Heesch numbers, no one knows whether there is any bound on the smallest translational unit a shape might require before it can be repeated to tile the plane. Myers discovered the current record holder, a shape whose simplest translational unit contains 10 tiles.

Credit: Jen Christiansen
When Smith began experimenting with the hat, what caught his eye was that it refused to conform to either of these options. The hat did not obviously tile the plane: he couldn't find a way to build a translational unit of any size. But it did not obviously fail to tile the plane, either: with effort, he could surround a hat with multiple layers of copies without getting stuck. It was conceivable that the hat might be a nontiler with a high Heesch number or a periodic monotile with a large translational unit, but Smith knew that such cases were rare. He reached out to me because he also knew that there was one other possibility, one so extraordinary that it demanded to be considered in full.
About 60 years ago mathematicians started wondering whether there were sets of shapes that could only tile the plane without ever repeating periodically—that is, that someone could assemble copies into arbitrarily large patches without ever encountering a translational unit. Such a set is called aperiodic. Crucially, aperiodicity is a much stronger property than nonperiodicity. Lots of shapes, including a humble 2 × 1 rectangle, can admit tilings that are periodic as well as tilings that aren't periodic. Aperiodic sets have no possible periodic tilings.

Credit: Jen Christiansen
The notion of aperiodicity was first articulated by Hao Wang in the early 1960s, while he was a math professor at Harvard University. He was studying what we now call Wang tiles: square tiles with symbolic labels or colors on their edges that must be positioned so that neighboring squares have the same markings on their adjoining edges. (These labels are a convenient shorthand for equivalent rules that can be expressed geometrically.) Wang observed that if, given a set of tiles, one can find a rectangle whose top and bottom edges have the same sequence of labels and whose left and right edges also match, then that rectangle is a translational unit, and hence the set tiles the plane. He then conjectured the converse: that if a set of Wang tiles admits a tiling of the plane, then it must be possible to build such a rectangle. In other words, he claimed that Wang tiles can never be aperiodic.
Based on what was known about tilings at the time, Wang's conjecture was quite reasonable. Building on this work a few years later, however, Wang's student Robert Berger disproved the conjecture by constructing the first aperiodic tile set, a sprawling system of 20,426 Wang tiles. In passing, Berger speculated that it should be possible to construct smaller aperiodic sets, inaugurating an irresistible mathematical quest to see how small a set could be. By 1971 Raphael M. Robinson of the University of California, Berkeley, had gotten down to a set of six modified squares.
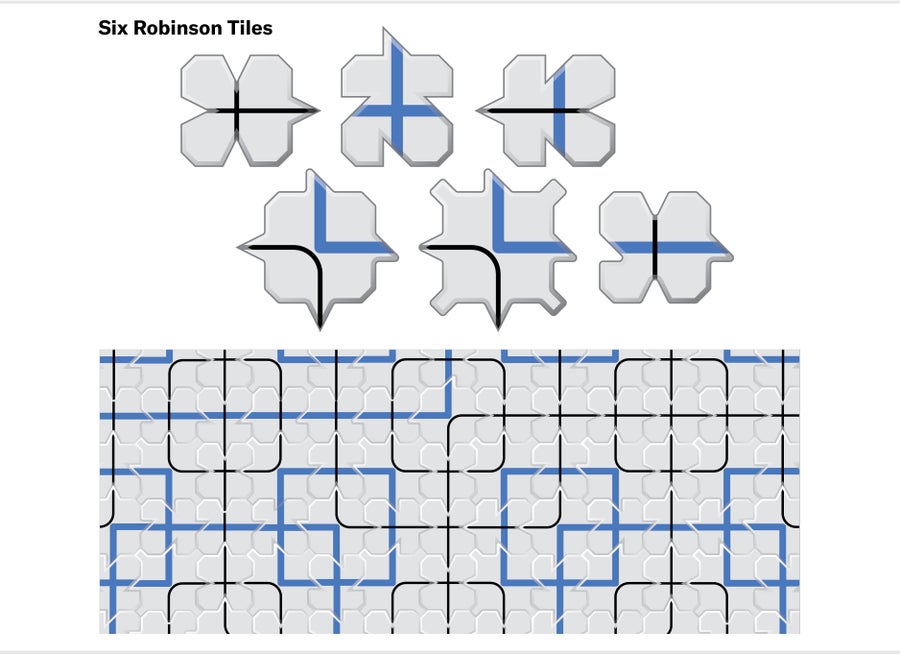
Credit: Jen Christiansen
Then, in 1973, University of Oxford mathematician Roger Penrose achieved a stunning breakthrough with a set of just two tiles: the “kite” and the “dart.”
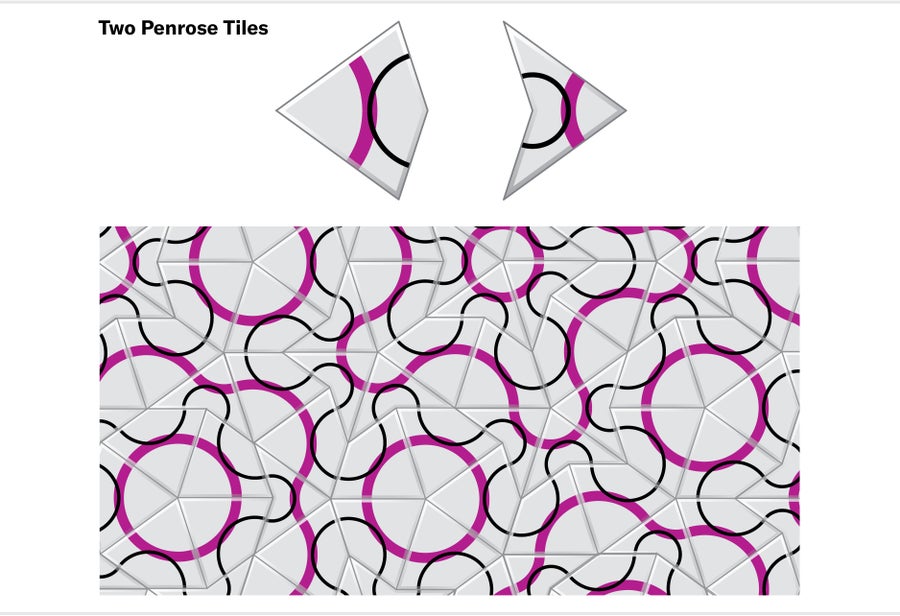
Credit: Jen Christiansen
Penrose's work left us one step short of an obvious finish line: an aperiodic monotile, a single shape that admits only nonperiodic tilings. Such a shape is also sometimes called an “einstein,” from the German “ein stein,” meaning “one stone.” (It's a pun on the name “Einstein” but otherwise has no connection to the famous Albert.) The question of whether an aperiodic monotile exists has been called the einstein problem.
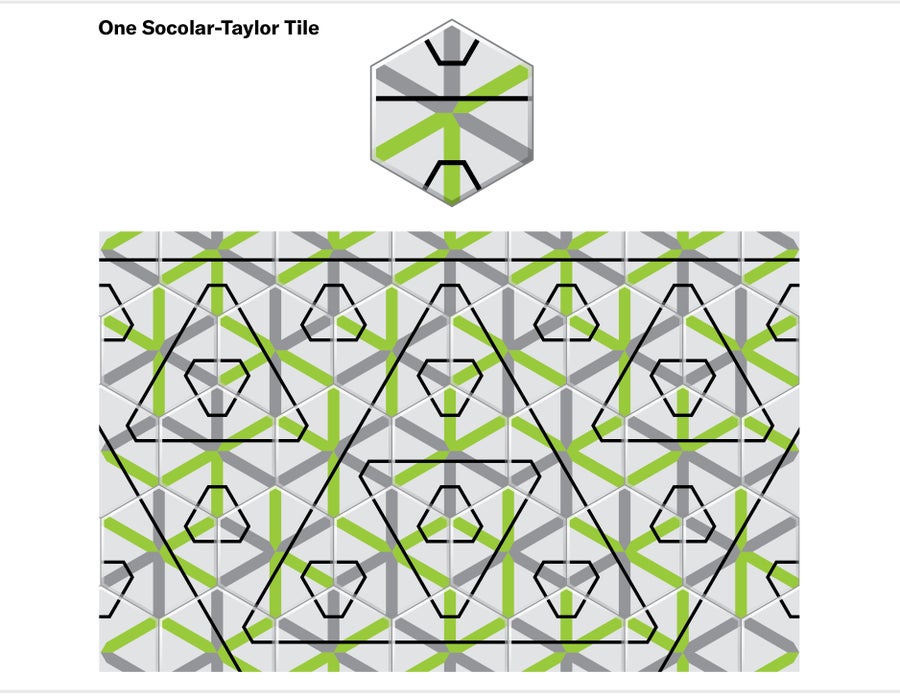
After Penrose, progress stalled for nearly 50 years. A few other sets of size two were discovered, including one by Goodman-Strauss. Some mathematicians proposed single-shape solutions, but these inevitably required small amendments to the rules of the game. For example, the Socolar-Taylor tile is a modified regular hexagon that tiles aperiodically. The catch is that for copies of this hexagon to conspire to force all tilings to be aperiodic, nonadjacent tiles must come to an agreement about their relative orientations. There is no way to bake this restriction into the outline of the tile without introducing a trick, such as extruding the hexagon into three dimensions or breaking it into disconnected pieces.
Credit: Jen Christiansen
Even when a problem in mathematics is unsolved, there is often a broad consensus among mathematicians about its likely answer. For example, Goldbach's conjecture states that every even number greater than two is the sum of two odd primes. This conjecture is unproven, but the evidence we have overwhelmingly suggests that it's correct. One reason I was always fascinated by the einstein problem is that I did not see clear evidence for or against it (apart from the grim reality of a 50-year dry spell). Some mathematicians were resigned to the impossibility of aperiodic monotiles, but I was open to either outcome. If nothing else, I suspected that an existence proof would be more tractable than a nonexistence proof. The former was likely to be an argument about the properties of a specific shape, but the latter would necessarily be a statement about all shapes. As we now know, in this instance there is some justice in the universe.
Smith hadn't specifically set out to find an aperiodic monotile, but he was aware of the history and significance of the problem. He was always on the lookout for signs of aperiodicity in his explorations. It was Smith who first dared to suggest, in an e-mail on November 24, 2022, that the hat might be an einstein, modestly adding, “Now wouldn't that be a thing?”
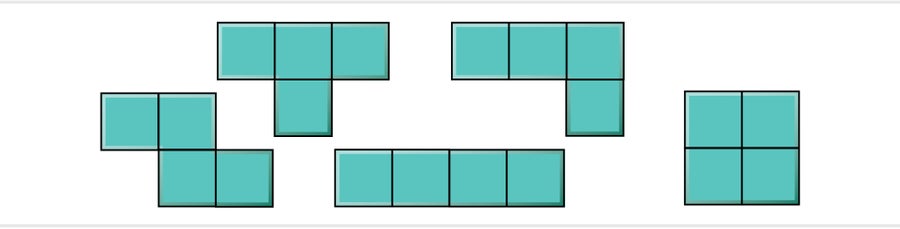
Smith and I began trying to understand the hat's behavior. The hat is what's known as a polyform: a shape made up of copies of some simple unit element. For example, the pieces in the video game Tetris represent all the ways to stick four squares together.
Credit: Jen Christiansen
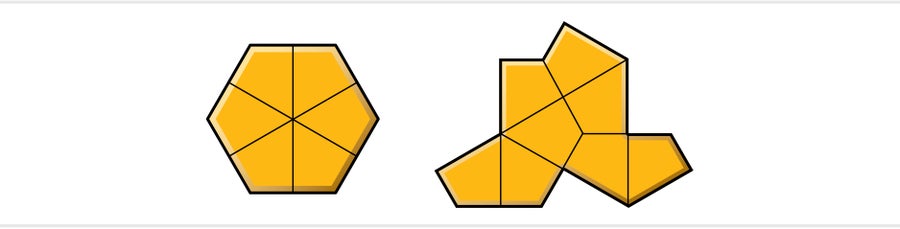
The hat is made from eight kites. These kites aren't the same as Penrose's; Smith made them by slicing a regular hexagon into six equal pieces with lines connecting the midpoints of opposite edges.
Credit: Jen Christiansen
He knew that I had recently written software to compute Heesch numbers of polyominoes (glued-together squares), polyhexes (regular hexagons) and polyiamonds (equilateral triangles), and he wondered whether it could be adapted to polykites. Fortunately, I had added support for kites the year before with the help of Ava Pun, an undergraduate at the University of Waterloo.
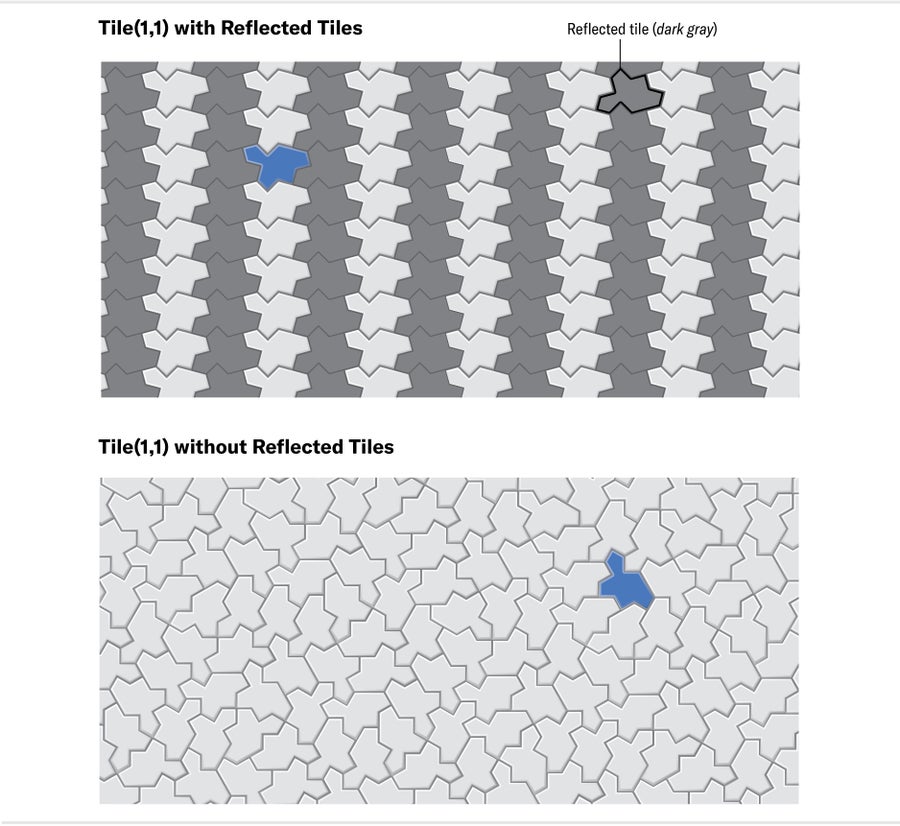
My software easily generated large clusters of hats without getting stuck, reinforcing our belief that the hat tiled the plane. Better yet, these new computer-generated clusters became raw data that Smith and I could study to refine our intuition. We began grouping hats in different ways, usually coloring them by hand in digital illustrations, to search for order. Recurring patterns leaped out immediately, organized around a sparse arrangement of reflected hats embedded in a larger field of unreflected hats (something Smith had also observed in his paper experiments).

Credit: Jen Christiansen
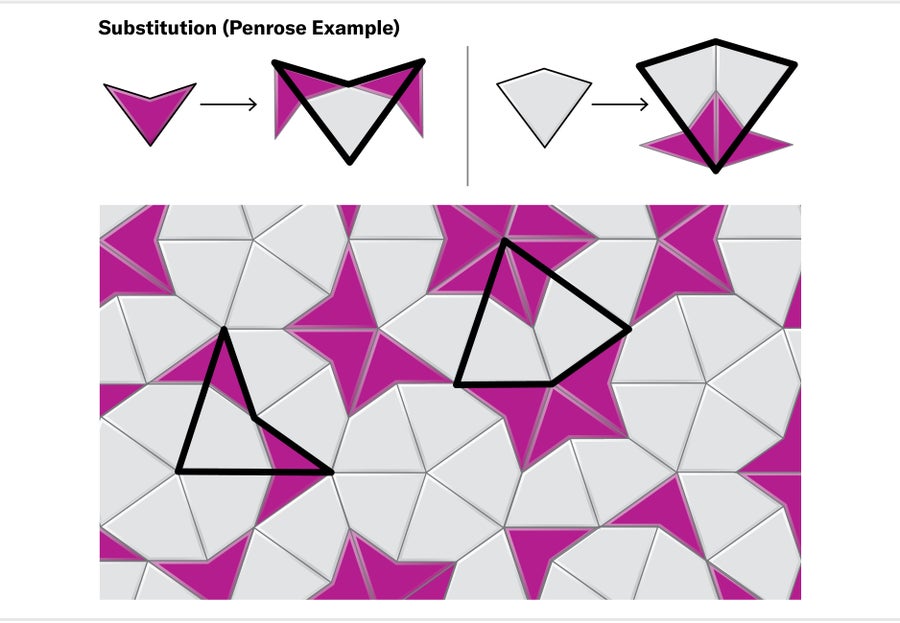
Yet these patterns never formed a translational unit. Moreover, the tiles seemed to build up into families of related “motifs” at multiple scales. This kind of recurring hierarchy hinted at a best-case scenario for eventually proving the hat was aperiodic: we could hope to find a system of so-called substitution rules. In a substitution system, every tile shape in a set is equipped with a rule that can be applied to replace it by a collection of smaller copies of the tiles. Armed with a suitable substitution system for hats, we might be able to start with a “seed” configuration of tiles and apply the rules iteratively, zooming in as we go to preserve scale. In this way, we would define a sequence of ever-larger clusters of hats, which would eventually fill the entire plane. Many aperiodic tile sets, including Penrose's, can be shown to tile the plane with substitution systems like these.
Credit: Jen Christiansen
On my 50th birthday, about two weeks after I first saw the hat, I found a preliminary set of substitution rules. The trick was to avoid working directly with “naked,” or single, reflected hats, which necessarily behaved differently than their unreflected counterparts. Instead I grouped each reflected hat with three of its neighbors to form an indivisible unit, a new “metatile” that could be treated as a full-fledged tile shape with a substitution rule of its own. I refined the metatiles and their rules through the rest of 2022, arriving at a system of four metatiles, each one a kind of schematic representation of a small cluster of hats.
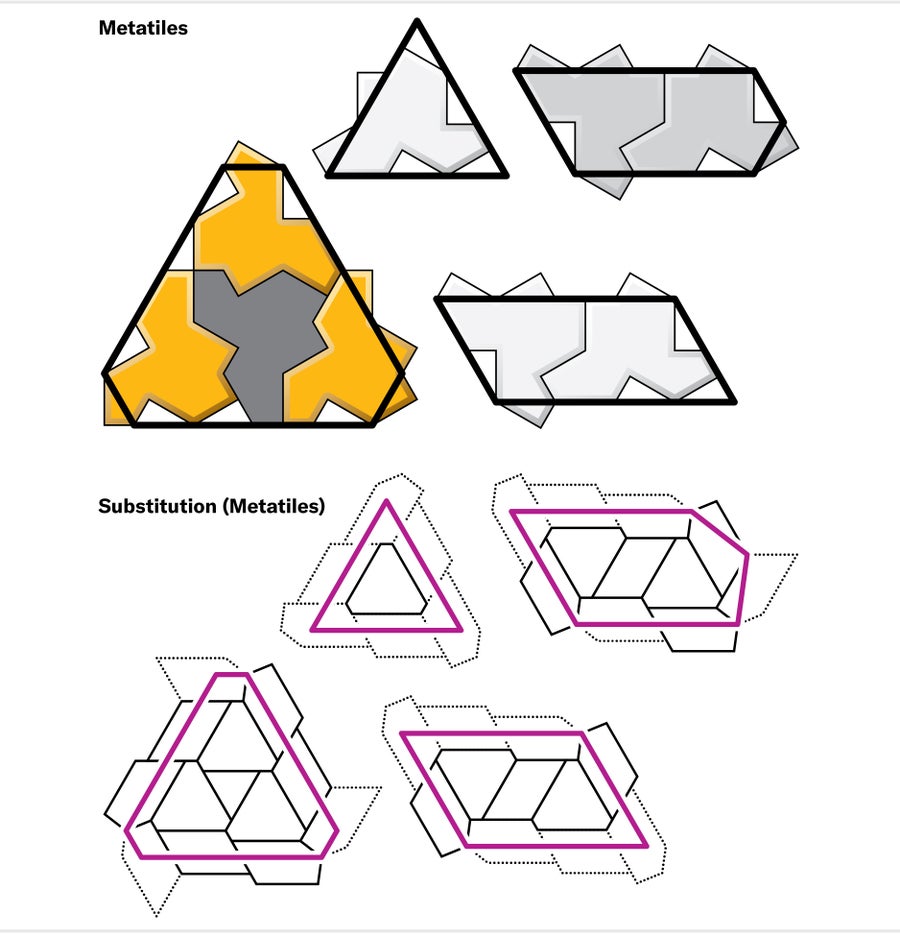
Credit: Jen Christiansen
By the start of 2023 Smith and I had half of a proof of aperiodicity, and arguably it was the easy half. Our metatiles and substitution rules guaranteed that the hat was a monotile: it tiled the infinite plane rather than petering out with an unexpectedly large, but finite, Heesch number. And it was easy to see that the tilings generated by the rules were nonperiodic. But remember that nonperiodicity is a far cry from aperiodicity. Perhaps our rules were just an overly complicated way to construct hat tilings, and periodic tilings existed, too. To complete the proof, we had to show that every tiling by hats was necessarily nonperiodic. I had some inkling of how that step might play out, but I felt as I imagine Smith had the previous November: close to the limits of my mathematical expertise. It was time to call in reinforcements.
Early in January 2023 Smith and I reached out to Goodman-Strauss, a mathematician who has published many important articles about tiling theory. I consider him a go-to authority on contemporary research. He is also known as a mathematics communicator and an organizer of hands-on activities, and at the time he was transitioning into a new role as an outreach mathematician at the National Museum of Mathematics in New York City. In other words, he was already swamped. But he provided valuable input and insisted that we also contact Myers immediately. Myers left academia after receiving a Ph.D. in the mathematical field of combinatorics, but he remained interested in tilings. In particular, he maintained a long-term project to catalog the tiling properties of polyforms. I had run some supporting computations for him back in 2006, and I was using his software as part of my own research on Heesch numbers.
I hadn't worked that closely with Myers before, so I was unprepared for his combination of mental horsepower, coding skill and knowledge of the field. His previous work on tilings had left him perfectly prepared for this moment. A mere eight days after being introduced to our work in progress, Myers completed the proof, confirming in late January that the hat was the world's first aperiodic monotile.
Before Myers came onboard, we already had our substitution rules and could generate tilings; his mission was to prove that all tilings by the hat had to be nonperiodic. In the aperiodicity playbook, the standard move at this point is to show that any tiling bears the imprint of the substitution rules. In other words, he needed to prove that for any arbitrary hat tiling, there is a unique way to group tiles into metatiles, metatiles into supertiles, and so on forever, reverse-engineering an infinite tower of substitutions that ends with the full, infinite tiling. A preexisting mathematical argument then would allow us to conclude that the tiling must be nonperiodic. The challenge of this strategy is to locate this tower atop an arbitrary hat tiling whose construction was not constrained at the outset to obey our rules.
Myers developed a computer-assisted approach to solving this problem. We generated an exhaustive list of 188 small clusters of tiles that could appear in hat tilings. These clusters represented every legal arrangement around a single hat so that each tile in any conceivable tiling must lie at the center of one such cluster. Myers then showed that each of these clusters could be divided up in a unique way into fragments of the metatiles, implying that the hats in any tiling could be grouped to yield a tiling by metatiles. Finally, he demonstrated that in a tiling made of metatiles, it was always possible to group metatiles into larger clusters called supertiles, which behave exactly like larger metatiles. This last step launches a kind of recursion: because the supertiles behave just like metatiles, the same grouping process applies to them as well. Once we group hats into metatiles and metatiles into supertiles, all subsequent levels of the hierarchy lock into place with a single mathematical flourish.
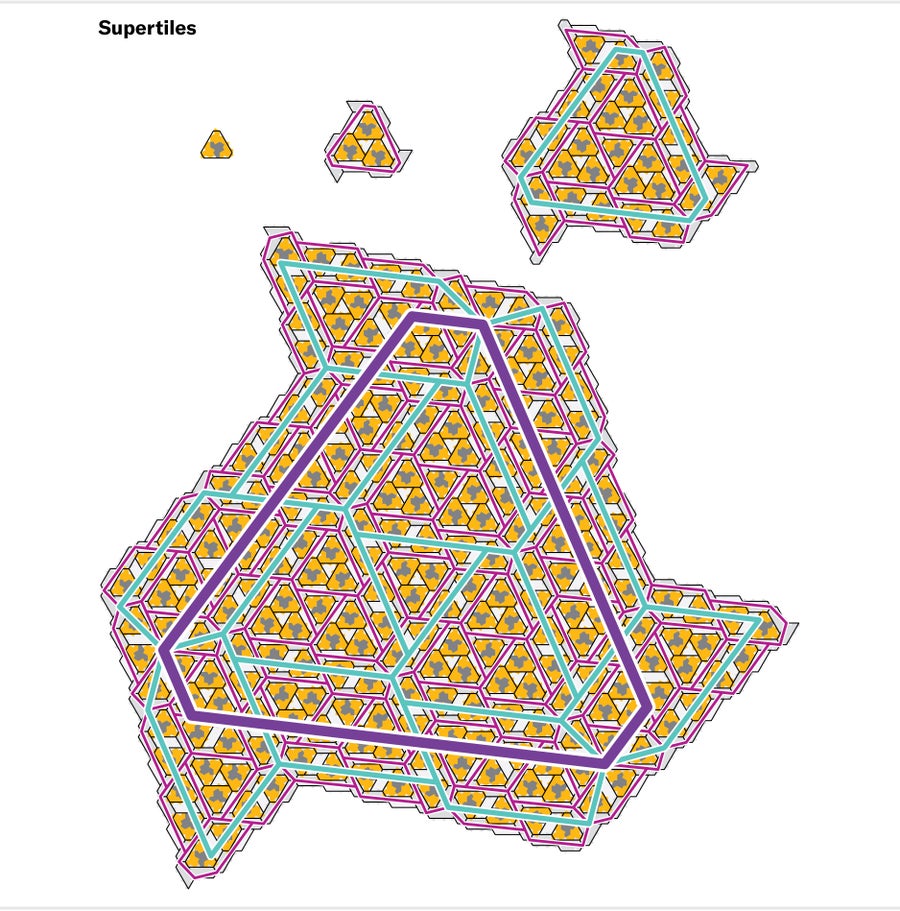
Credit: Jen Christiansen
We had our prize, and in early February 2023 we began writing a manuscript to share the hat with the world. That might have been the end to an already magical story were it not for Smith's capacity for mathematical discovery. Way back in December 2022 he had shocked me by e-mailing me a second shape, a polykite we call the turtle, which behaved a lot like the hat. The turtle, too, radiated an uncanny aura of aperiodicity. Was it possible that Smith had discovered two revolutionary shapes in two weeks after others had looked in vain for 50 years? I begged for patience; my head was already full of hats, so to speak.
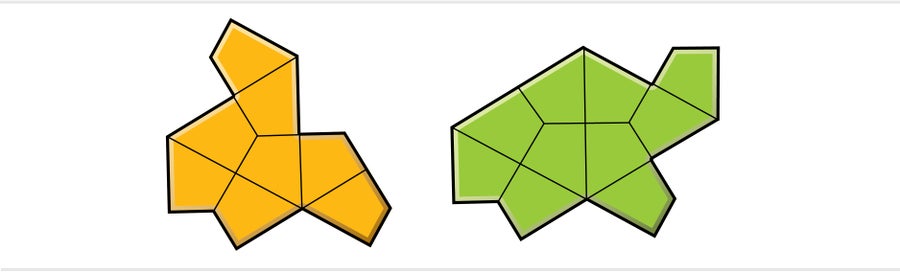
Credit: Jen Christiansen
But after resolving the status of the hat, Myers began contemplating the neglected turtle. A week or two later he stunned the three of us with the observation that the turtle was necessarily also aperiodic because it was really just a hat in disguise. In fact, the hat and the turtle were two shapes in a continuous family of polygons, all of which were aperiodic and tiled in the same way.

Credit: Jen Christiansen
The hat can be regarded as a polygon with edges of length 1 and √3 (where two consecutive edges of length 1 form one longer edge). Just as one can construct a family of rectangles by varying the lengths of its horizontal and vertical edges independently, we can choose any two numbers a and b to replace the hat's edge lengths and obtain a new polygon that we will call Tile(a,b). Using this notation, the hat is Tile(1,√3 ), and the turtle is Tile(√3 ,1). Myers showed that nearly all shapes of the form Tile(a,b) are aperiodic monotiles with the same tilings. There were just three exceptions: Tile(0,1) (the “chevron”), Tile(1,0) (the “comet”) and the equilateral polygon Tile(1,1) (which never acquired a catchy nickname). Each of these three shapes is more flexible, admitting both periodic and nonperiodic tilings.
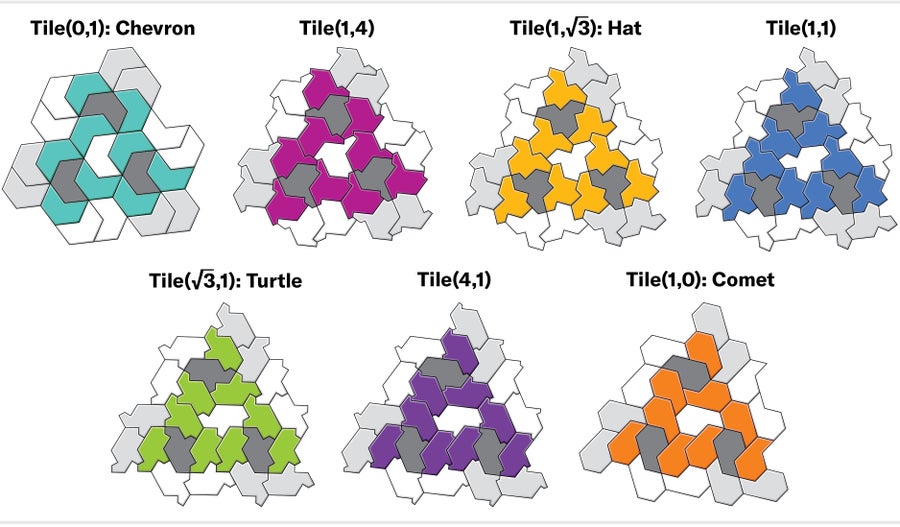
Credit: Jen Christiansen
Soon after, Myers doubled down on the link he had forged between the hat and the turtle, developing a remarkable second proof of the hat's aperiodicity based on the Tile(a,b) continuum. He relied on the classic technique of proof by contradiction: he posited the existence of a periodic tiling of hats, and then, from the existence of such a tiling, he derived an absurdity that showed the initial supposition (the periodic hat tiling) was impossible. Specifically, he found that one could stretch and squeeze edges in a periodic hat tiling to obtain equivalent, periodic tilings by chevrons and comets. But chevrons and comets are both polyiamonds (unions of equilateral triangles) built on top of regular triangular tilings at different scales. In an argument that involves combinatorics, geometry and a dash of number theory, Myers proved that because the chevron and comet tilings originated from the same supposedly periodic hat tiling, their underlying triangle tilings would have to be related to each other through a mathematically impossible scaling factor. This was a second way to prove that the hat is an aperiodic monotile. It's exciting not just because it bolsters the claim of the hat's aperiodicity but also because it represents a whole new method of proof in this field, which could be useful in analyzing other tiles in the future.
We put our manuscript online in March 2023 and received an enthusiastic, overwhelming response from mathematicians and tiling hobbyists. The hat became an immediate source of inspiration for artists, designers and puzzle creators (you can now buy hat tiling sets on Etsy, for instance). It's important to remember that the work has not yet emerged from the crucible of peer review, although it has withstood a great deal of scrutiny from experts with barely a scratch.
When we first revealed the hat, people objected to one aspect of our work more frequently than any other: the use of reflected tiles. Every tiling by hats must include a sparse distribution of reflected hats, as Smith and I discovered early on. Mathematically, this objection does not derail our result: the accepted definition of a monotile has always allowed reflections as legal moves in tilings. Still, many wondered, could there be a shape out there that yields a “one-handed,” or “chiral,” aperiodic tiling in which no tiles are flipped over? Our manuscript offered no insight into this problem, and we were as prepared as everyone else to settle in for the long wait until its resolution.
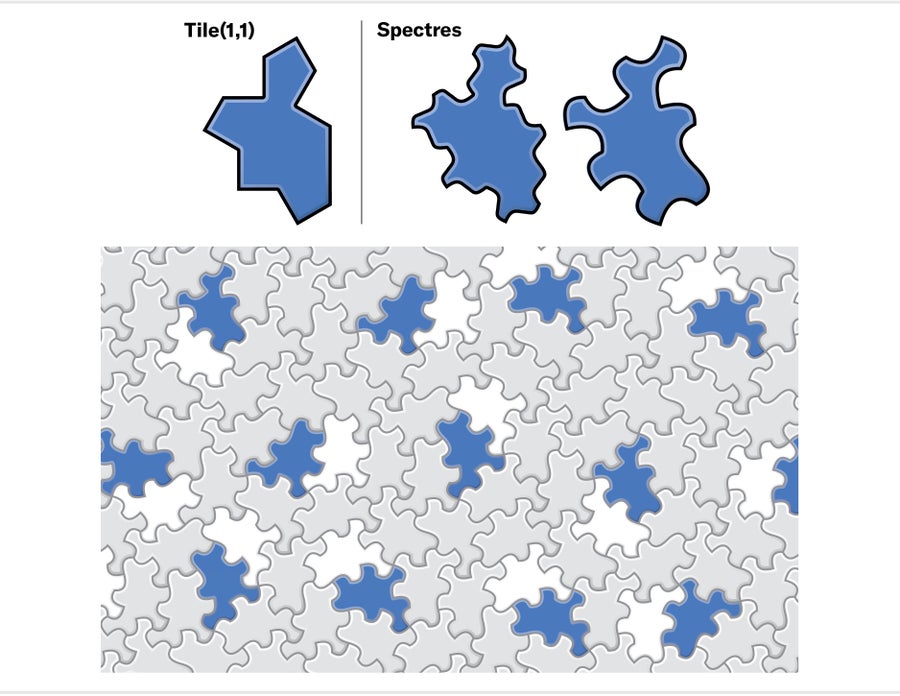
Happily, Smith had one more astounding surprise for us. Less than a week after our first manuscript went live, he began e-mailing the rest of us about Tile(1,1), the equilateral member of the continuum of shapes that included the hat and the turtle. We knew that this polygon was not aperiodic: it admitted periodic tilings that mixed unreflected and reflected tiles. But Smith observed that if he deliberately restricted himself to tiles of a single-handedness (no flipping allowed), he produced intriguing clusters of tiles.
Credit: Jen Christiansen
The four of us immediately dove into a new collaboration. We computed large patches of unreflected copies of Tile(1,1) and studied them for patterns. We discovered a way to group tiles into recurring clusters and then determined substitution rules for those clusters that yielded superclusters with identical behavior. Once again, this recursive grouping guaranteed the existence of a unique infinite hierarchy of substitutions that forced all unreflected (single-handed) tilings to be nonperiodic. The final trick was simply to replace the edges of Tile(1,1) with arbitrary curves, which guaranteed that tiles and their reflections couldn't coexist in a tiling. The result was a family of shapes that we called spectres, all of which turned out to be chiral aperiodic monotiles.
Credit: Jen Christiansen
There is a romance to stories of mathematicians working for years on intractable problems, sometimes in secret, and finally emerging into the light with a new result. That is not our story. Although I was always fascinated by the einstein problem, I never worked on it directly—I started only when I was handed the answer in November 2022. The hat more or less materialized in Smith's hands, and I was lucky that he chose to contact me. A few months later we had a complete proof, created through a process that was, as far as I can tell, painless for all four of us. Perhaps our pace reflects the fact that there is a clear procedure to follow in generating a proof of aperiodicity if you have the right shape to begin with. Our sense of ease was also surely a result of the decades we had each spent pondering the einstein problem and related questions. That experience left us well positioned to recognize the hat as a possible solution and to know what to do with it.
There is no shortage of unsolved problems in tiling theory, a branch of mathematics with a low barrier to entry and lots of visual appeal. Smith joins a pantheon of enthusiastic amateurs who have made important contributions to the field, often after reading about open problems in this magazine. He is in the company of Robert Ammann, who independently discovered many of the same results as Penrose and contributed other important ideas to tiling theory; Marjorie Rice, who discovered new classes of pentagonal monotiles; and Joan Taylor, who originated the Socolar-Taylor tile. I should also include the artist M. C. Escher, who invented the math he needed to draw his tessellations, even if he would not have thought of it as math at all.
As the impact of our aperiodic monotiles ripples outward, I'm sure it will stimulate new scholarly research. But I hope we also entice others who might have seen mathematics as forbidding but now recognize an opportunity to play.

Credit: Miriam Martincic

