A Weird Form of Dark Energy Might Solve a Cosmic Conundrum

Fifteen years ago cosmologists were flying high. The simple but wildly successful “standard model of cosmology” could, with just a few ingredients, account for a lot of what we see in the universe. It seemed to explain the distribution of galaxies in space today, the accelerated expansion of the universe and the fluctuations in the brightness of the relic glow from the big bang—called the cosmic microwave background (CMB)—based on a handful of numbers fed into the model. Sure, it contained some unexplained exotic features, such as dark matter and dark energy, but otherwise everything held together. Cosmologists were (relatively) happy.

Over the past decade, though, a pesky inconsistency has arisen, one that defies easy explanation and may portend significant breaks from the standard model. The problem lies with the question of how fast space is growing. When astronomers measure this expansion rate, known as the Hubble constant, by observing supernovae in the nearby universe, their result disagrees with the rate given by the standard model.

This “Hubble tension” was first noted more than 10 years ago, but it was not clear then whether the discrepancy was real or the result of measurement error. With time, however, the inconsistency has become more firmly entrenched, and it now represents a major thorn in the side of an otherwise capable model. The latest data, from the James Webb Space Telescope (JWST), have made the problem worse.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

The two of us have been deeply involved in this saga. One (Riess) is an observer and co-discoverer of dark energy, one of the last pieces of the standard cosmological model. He has also spearheaded efforts to determine the Hubble constant by observing the local universe. The other (Kamionkowski) is a theorist who helped to figure out how to calculate the Hubble constant by measuring the CMB. More recently he helped to develop one of the most promising ideas to explain the discrepancy—a notion called early dark energy.

One possibility is that the Hubble tension is telling us the baby universe was expanding faster than we think. Early dark energy posits that this extra expansion might have resulted from an additional repulsive force that was pushing against space at the time and has since died out.

This suggestion is finally facing real-world tests, as experiments are just now becoming capable of measuring the kinds of signals early dark energy might have produced. So far the results are mixed. But as new data come in over the next few years, we should learn more about whether the expansion of the cosmos is diverging from our predictions and possibly why.

The idea that the universe is expanding at all came as a surprise in 1929, when Edwin Hubble used the Mount Wilson Observatory near Pasadena, Calif., to show that galaxies are all moving apart from one another. At the time many scientists, including Albert Einstein, favored the idea of a static universe. But the separating galaxies showed that space is swelling ever larger.

If you take an expanding universe and mentally rewind it, you reach the conclusion that at some finite time in the past, all the matter in space would have been on top of itself—the moment of the big bang. The faster the rate of expansion, the shorter the time between that big bang and today. Hubble used this logic to make the first calculation of the Hubble constant, but his initial estimate was so high that it implied the universe was younger than the solar system. This was the very first “Hubble tension,” which was later resolved when German astronomer Walter Baade discovered that the distant galaxies Hubble used for his estimate contained different kinds of stars than the nearby ones he used to calibrate his numbers.

A second Hubble tension appeared in the 1990s as a result of sharpening observations from the Hubble Space Telescope. The observatory’s measured value of the Hubble constant implied that the universe’s oldest stars were older than stellar-evolution theories suggested. This tension was resolved in 1998 with the discovery that the expansion of the cosmos was accelerating. This shocking revelation led scientists to add dark energy—the energy of empty space—to the standard model of cosmology. Once researchers understood that the universe is expanding faster now than it did when it was young, they realized it had to be several billion years older than previously thought.

One possible explanation is that the Hubble tension is telling us the baby universe was expanding faster than we think.

Since then, our understanding of the origin and evolution of the universe has changed considerably. We can now measure the CMB—our single greatest piece of evidence about cosmic history—with a precision unimaginable at the turn of the millennium. We have mapped the distribution of galaxies over cosmic volumes hundreds of times larger than we had then. Likewise, the number of supernovae being used to measure the expansion history has reached several thousand.

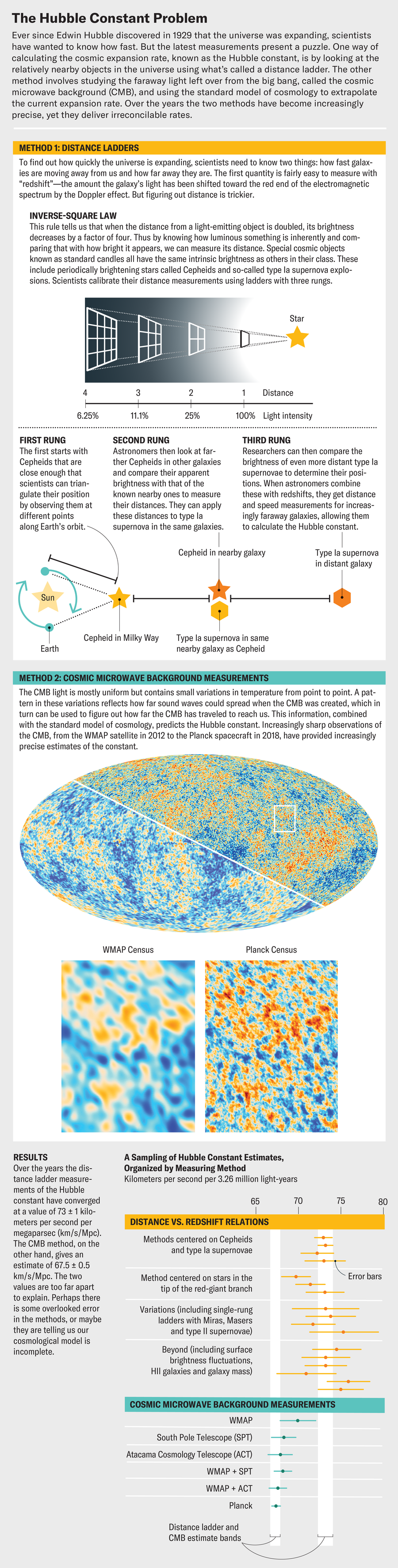
Yet our estimates of how fast space is growing still disagree. For more than a decade increasingly precise measurements of the Hubble constant based on the local universe, made without reference to the standard model and therefore directly testing its accuracy, have converged around 73 kilometers per second per megaparsec (km/s/Mpc) of space, plus or minus 1. This figure is too large, and its estimated uncertainty too small, to be compatible with the value the standard model predicts based on CMB data: 67.5 ± 0.5 km/s/Mpc.

The local measurements are largely based on observations of supernovae in a certain class, type Ia, that all explode with a similar energy output, meaning they all have the same intrinsic brightness, or luminosity. Their apparent luminosity (how bright they appear in the sky) is a proxy for their distance from Earth. And comparing their distance with their speed—which we get by measuring their redshift (how much their light has been shifted toward the red end of the electromagnetic spectrum)—tells us how fast space is expanding.

Astronomers calibrate their type Ia supernova distance measurements by comparing them with values for nearby galaxies that host both a supernova of this type and at least one Cepheid variable star—a pulsating supergiant that flares on a timescale tightly correlated to its luminosity, a fact discovered a century ago by Henrietta Swan Leavitt. Scientists in turn calibrate this period-luminosity relation by observing Cepheids in very nearby galaxies whose distances we can measure geometrically through a method called parallax. This step-by-step calibration is called a distance ladder.

Twenty-five years ago a landmark measurement of this kind came out of the Hubble Key Project, resulting in a Hubble constant measurement of H₀ = 72 ± 8 km/s/Mpc. About a dozen years ago this value improved to 74 ± 2.5 km/s/Mpc, thanks to work by two independent groups (the SH0ES team, led by Riess, and the Carnegie Hubble Program, led by Wendy L. Freedman of the University of Chicago). In the past few years these measurements have been replicated by many studies and further refined with the aid of the European Space Agency Gaia parallax observatory to 73 ± 1. Even if we replace some of the steps in the parallax-Cepheid-supernova calibration sequence with other estimates of stellar distances, the Hubble constant changes little and cannot be brought below about 70 km/s/Mpc without uncomfortable contrivances or jettisoning most of the Hubble Space Telescope data. Even this lowest value, though, is far too large compared with the number inferred from the CMB to be chalked up to bad luck.

Astronomers have worked through a long list of possible problems with the supernova distances and suggested many follow-up tests, but none have revealed a flaw in the measurements. Until recently, one of the remaining concerns involved how we determine Cepheid brightness in crowded fields of view. With the Hubble Space Telescope, some of the light from any given Cepheid star overlapped with light from other stars close to it, so scientists had to use statistics to estimate how bright the Cepheid was alone. Recently, however, JWST allowed us to reimage some of these Cepheids with dramatically improved resolution. With JWST, the stars are very cleanly separated with no overlap, and the new measurements are fully consistent with those from Hubble.

The method for inferring the Hubble constant from the CMB is a bit more involved but is based on similar principles. The intensity of the CMB light is very nearly the same everywhere in space. Precise measurements show, however, that the intensity varies from one point to another by roughly one part in 100,000. To the eye, this pattern of intensity variations appears fairly random. Yet if we look at two points that are separated by around one degree (about two full moons side by side on the sky), we see a correlation: their intensities (temperatures) are likely to be similar. This pattern is a consequence of how sound spread in the early universe.

During the first roughly 380,000 years after the big bang, space was filled with a plasma of free protons, electrons and light. At around 380,000 years, though, the cosmos cooled enough that electrons could combine with protons to form neutral hydrogen atoms for the first time. Before then electrons had zoomed freely through space, and light couldn’t travel far without hitting one. Afterward the electrons were bound up in atoms, and light could flow freely. That initial release of light is what we observe as the CMB today.

During those first 380,000 years, small changes in the density of the electron-proton-light plasma that filled space spread as sound waves, just as sound propagates through the air in a room. The precise origin of these sound waves has to do with quantum fluctuations during the very early universe, but we think of them as noise left over from the big bang. A cosmological sound wave travels a distance determined by the speed of sound in a medium multiplied by the time since the big bang; we call this distance the sound horizon. If there happened to be a particularly “loud” spot somewhere in the universe at the big bang, then it will eventually be “heard” at any point that is a sound horizon away. When the CMB light was released at 380,000 years, it was imprinted with the intensity of the soundscape at that point. The one-degree scale correlation in the CMB intensity thus corresponds to the angular size of the sound horizon at that time.

That scale is determined by the ratio of the sound horizon to the distance to the “surface of last scatter”—essentially, how far light has traveled since it was freed when the CMB was released (the moment electrons were all bound up in atoms, and light could travel freely for the first time). If the expansion rate of the universe is larger, then that distance is smaller, and vice versa.

Astronomers can therefore use the measurement of the sound horizon to predict the current rate of the universe’s expansion—the Hubble constant. The standard model of cosmology predicts a physical length for the sound horizon based on the gravitationally attracting ingredients of the early universe: dark matter, dark energy, neutrinos, photons and atoms. By comparing this length with the measured angular length of the horizon from the CMB (one degree), scientists can infer a value for the Hubble constant. The only problem is that this CMB-inferred value is smaller, by about 9 percent, than the number we obtain by using supernovae.

Had the CMB-inferred value turned out to be larger than the local value, we would have had a fairly obvious explanation. The distance to the surface of last scatter also depends on the nature of dark energy. If the dark energy density is not precisely constant but decreases slowly with time (as some models, such as one called quintessence, propose), then the distance to the surface of last scatter will be decreased, bringing the CMB-based value of the Hubble constant down to the value observed locally.

Conversely, if the dark energy density were slowly increasing with time, then we would infer from the CMB a larger Hubble constant, and there would be no tension with the supernova measurements. Yet this explanation requires that energy somehow be created out of nothing—a violation of energy conservation, which is a sacred principle in physics. Even if we are perverse enough to imagine models that don’t respect energy conservation, we still can’t seem to resolve the Hubble tension. The reason has to do with galaxy surveys. The distribution of galaxies in the universe today evolved from the distribution of matter in the early cosmos and thus exhibits the same sound-horizon bump in its correlations. The angular scale of that correlation also allows us to infer distances to the same types of galaxies that host supernovae, and these distances (using the same sound horizon as employed for the CMB) give us a low value of the Hubble constant, consistent with the CMB.

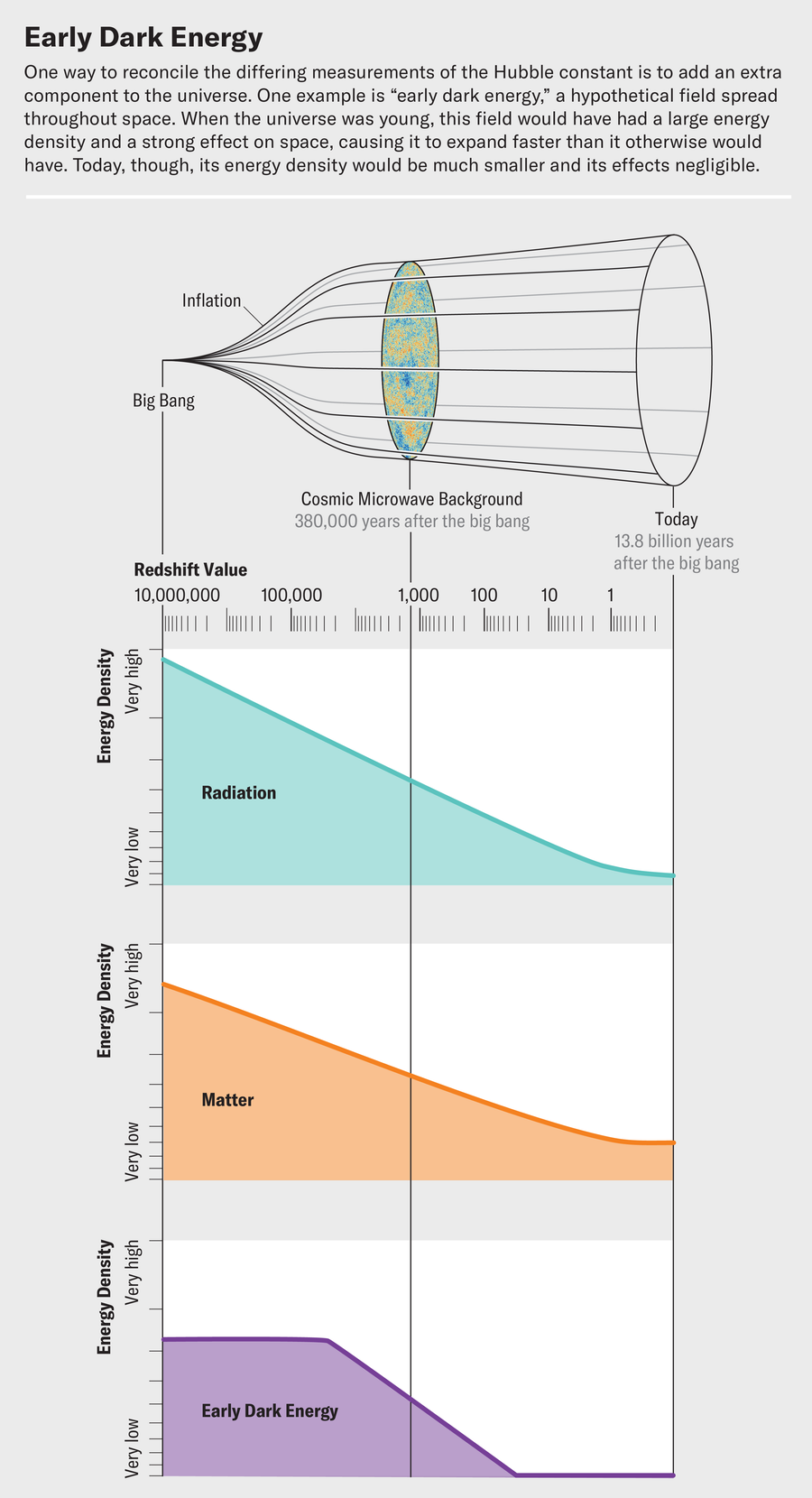
We’re left to conclude that “late-time” solutions for the Hubble tension—those that attempt to alter the relation between the Hubble constant and the distance to the CMB surface of last scattering—don’t work or at least are not the whole story. The alternative, then, is to surmise that there may be something missing in our understanding of the early universe that leads to a smaller sound horizon. Early dark energy is one possibility.

Kamionkowski and his then graduate student Tanvi Karwal were the first to explore this idea in 2016. The expansion rate in the early universe is determined by the density of all the matter in the cosmos at the time. In the standard cosmological model, this includes photons, dark energy, dark matter, neutrinos, protons, electrons and helium nuclei. But what if there were some new component of matter—early dark energy—that had a density roughly 10 percent of the value for everything else at the time and then later decayed away?

The most obvious form for early dark energy to take is a field, similar to an electromagnetic field, that fills space. This field would have added a negative-pressure energy density to space when the universe was young, with the effect of pushing against gravity and propelling space toward a faster expansion. There are two types of fields that could fit the bill. The simplest option is what’s called a slowly rolling scalar field. This field would start off with its energy density in the form of potential energy—picture it resting on top of a hill. Over time the field would roll down the hill, and its potential energy would be converted to kinetic energy. Kinetic energy wouldn’t affect the universe’s expansion the way the potential energy did, so its effects wouldn’t be observable as time went on.

A second option is for the early dark energy field to oscillate rapidly. This field would quickly move from potential to kinetic energy and back again, as if the field were rolling down a hill, into a valley, up another hill and then back down again over and over. If the starting potential is chosen correctly, then the average leads to an overall energy density with more potential energy than kinetic energy—in other words, a situation that produces negative pressure against the universe (as dark energy does) rather than positive pressure (as ordinary matter does). This more complicated oscillating scenario is not required, but it can lead to a variety of interesting physical consequences. For instance, an oscillating early dark energy field might give rise to particles that could be new dark matter candidates or might provide additional seeds for the growth of a large cosmic structure that could show up in the later universe.

After their initial suggestion of early dark energy in 2016, Kamionkowski and Karwal, along with Vivian Poulin of the French National Center for Scientific Research (CNRS) and Tristan L. Smith of Swarthmore College, developed tools to compare the model’s predictions with CMB data. It’s hard to depart much from the standard cosmological model when we have such precise measurements of the CMB that so far match the model very well. We figured it was a long shot that early dark energy would actually work. To our surprise, though, the analysis identified classes of models that would allow a higher Hubble constant and still fit the CMB data well.

This promising start led others to create a proliferation of variants of early dark energy models. In 2018 these models fared about as well as the standard model in matching CMB measurements. But by 2021 new, higher-resolution CMB data from the Atacama Cosmology Telescope (ACT) seemed to favor early dark energy over the standard model, which drew even more scientists toward the idea. In the past three years, however, more measurements and analysis from ACT, as well as from the South Pole Telescope, the Dark Energy Survey and the Dark Energy Spectroscopic Instrument, led to more nuanced conclusions. Although some analyses keep early dark energy in the running, most of the results seem to be converging toward the standard cosmological model. Even so, the jury is still out: a broad array of imaginable early dark energy models remain viable.

Many theorists think it may be time to explore other ideas. The problem is that there aren’t any particularly compelling new ideas that seem viable. We need something that can increase the expansion of the young universe and shrink the sound horizon to raise the Hubble constant. Perhaps protons and electrons somehow combined differently to form atoms at that time than they do now, or maybe we’re missing some effects of early magnetic fields, funny dark matter properties or subtleties in the initial conditions of the early universe. Cosmologists will agree that simple explanations continue to elude us even as the Hubble tension becomes more firmly embedded in the data.

To progress, we must continue to find ways to scrutinize, check and test both local and CMB-inferred values of the Hubble constant. Astronomers are developing strategies for gauging local distances to augment the supernova-based approaches. Measurements of distances to quasars based on radio-interferometric techniques, for instance, are advancing, and there are prospects for using fluctuations in galaxy-surface brightness. Others are trying to use type II supernovae and different kinds of red giant stars to measure distances. There are even proposals to use gravitational-wave signals from merging black holes and neutron stars. We are also intrigued by the potential to determine cosmic distances with gravitational lensing.

Although current results are not yet precise enough to weigh in on the Hubble tension, we expect to see great progress when the Vera C. Rubin Observatory and the Nancy Grace Roman Space Telescope come online. For now we have no good answers, but lots of great questions and experiments are underway.